【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
参考答案:
【答案】B
【解析】
先求得直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),由
,0),由![]() 0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b
0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b![]() ;②若点M在点O和点A之间,求得
;②若点M在点O和点A之间,求得![]() b
b![]() ; ③若点M在点A的左侧,求得
; ③若点M在点A的左侧,求得![]() b>1
b>1![]() .再把以上得到的三个b的范围取并集,可得结果.
.再把以上得到的三个b的范围取并集,可得结果.
由题意可得,三角形ABC的面积为 ![]() 1,
1,
由于直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),
,0),
由直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,可得b>0,
故![]() 0,故点M在射线OA上.
0,故点M在射线OA上.
设直线y=ax+b和BC的交点为N,则由![]() 可得点N的坐标为(
可得点N的坐标为(![]() ,
,![]() ).
).
①若点M和点A重合,如图:

则点N为线段BC的中点,故N(![]() ,
,![]() ),
),
把A、N两点的坐标代入直线y=ax+b,求得a=b![]() .
.
②若点M在点O和点A之间,如图:
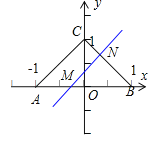
此时b![]() ,点N在点B和点C之间,
,点N在点B和点C之间,
由题意可得三角形NMB的面积等于![]() ,
,
即![]() ,即
,即 ![]() ,可得a
,可得a![]() 0,求得 b
0,求得 b![]() ,
,
故有![]() b
b![]() .
.
③若点M在点A的左侧,
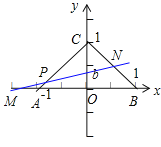
则b![]() ,由点M的横坐标
,由点M的横坐标![]() 1,求得b>a.
1,求得b>a.
设直线y=ax+b和AC的交点为P,则由 ![]() 求得点P的坐标为(
求得点P的坐标为(![]() ,
,![]() ),
),
此时,由题意可得,三角形CPN的面积等于![]() ,即
,即 ![]() (1﹣b)|xN﹣xP|
(1﹣b)|xN﹣xP|![]() ,
,
即![]() (1﹣b)|
(1﹣b)|![]() |
|![]() ,化简可得2(1﹣b)2=|a2﹣1|.
,化简可得2(1﹣b)2=|a2﹣1|.
由于此时 b>a>0,0<a<1,∴2(1﹣b)2=|a2﹣1|=1﹣a2 .
两边开方可得 ![]() (1﹣b)
(1﹣b)![]() 1,∴1﹣b
1,∴1﹣b![]() ,化简可得 b>1
,化简可得 b>1![]() ,
,
故有1![]() b
b![]() .
.
综上可得b的取值范围应是 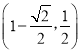 ,
,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一个平面内,向量
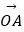 ,
, 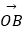 ,
, 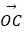 的模分别为1,1,
的模分别为1,1,  ,
, 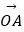 与
与 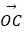 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, 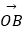 与
与 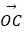 的夹角为45°.若
的夹角为45°.若 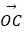 =m
=m 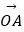 +n
+n 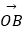 (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 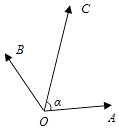
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=sin(ωx﹣
 )+sin(ωx﹣
)+sin(ωx﹣  ),其中0<ω<3,已知f(
),其中0<ω<3,已知f(  )=0.(12分)
)=0.(12分)
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣  ,
, 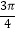 ]上的最小值.
]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=
 .
.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+ )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)求平行于直线3x+4y- 2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y -5=0且与点P( -1,0)的距离是
 的直线方程.
的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
 .
.(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记“
 ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;②在区间
 内任取2个实数
内任取2个实数 ,求事件“
,求事件“ 恒成立”的概率.
恒成立”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线 ,
, .
.(1)直线
 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;(2)已知点
 ,若直线
,若直线 上存在点
上存在点 满足条件
满足条件 ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

