【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
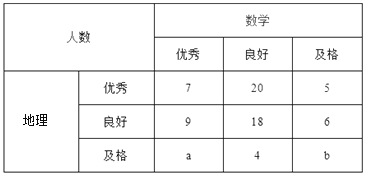
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
参考答案:
【答案】(Ⅰ)![]() 、
、![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析: (Ⅰ)根据优秀率定义,由样本中数学成绩优秀率,可得关于![]() 的等式,解得
的等式,解得![]() 的值; (Ⅱ)由(Ⅰ)知
的值; (Ⅱ)由(Ⅰ)知![]() ,又
,又![]() ,可列出所有满足条件的情况,找出其中数学成绩为优秀的人数比及格的人数少的组数,利用古典概型的定义,可求得所要求概率.
,可列出所有满足条件的情况,找出其中数学成绩为优秀的人数比及格的人数少的组数,利用古典概型的定义,可求得所要求概率.
试题解析:(Ⅰ)由题意得,![]() ,解得
,解得![]() ,
,
∵![]() ,
,
∴![]() .
.
(Ⅱ)由题意,知![]() ,且
,且![]() ,
,
∴满足条件的![]() 有:
有:![]() ,
,
![]() ,
,
![]() 共14组,且每组出现的可能性相同.
共14组,且每组出现的可能性相同.
其中数学成绩为优秀的人数比及格的人数少有:![]() 共6组.
共6组.
∴数学成绩为优秀的人数比及格的人数少的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0.
(1)求证:f(x)是奇函数;
(2)若f(1)=
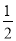 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用
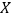 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量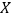 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府决定建造一批保障房供给社会,缓解贫困人口的住房问题,计划用1 600万元购得一块土地,在该土地上建造10幢楼房的住宅小区,每幢楼的楼层数相同,且每层建筑面积均为1 000平方米,每平方米的建筑费用与楼层有关,第x层楼房每平方米的建筑费用为(kx+800)元(其中k为常数).经测算,若每幢楼为5层,则该小区每平方米的平均综合费用为1 270元.
注:每平方米平均综合费用=
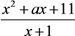 .
.(1) 求k的值;
(2) 问要使该小区楼房每平方米的平均综合费用最低,应将这10幢楼房建成多少层?此时每平方米的平均综合费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于( )
A. 0.5 B. -0.5
C. 1.5 D. -1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=loga(x+3)-1(a>0,a≠1)的图象恒过定点A.
(1) 求点A的坐标;
(2) 若点A在直线mx+ny+1=0上,其中m,n都是正数,求
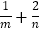 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 若x>1,求x+
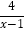 的最小值;
的最小值;(2) 若x>0,y>0,且2x+8y-xy=0,求xy的最小值.
相关试题

