

【题目】已知圆![]() ,
,![]() ,动圆
,动圆![]() 与圆
与圆![]() 、
、![]() 都相切,则动圆
都相切,则动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程为________;直线
的方程为________;直线![]() 与曲线
与曲线![]() 仅有三个公共点,依次为
仅有三个公共点,依次为![]() 、
、![]() 、
、![]() ,则
,则![]() 的最大值为________.
的最大值为________.
【答案】![]() 或
或![]()
![]()
【解析】
分两种情况讨论①圆![]() 与圆
与圆![]() 外切,与圆
外切,与圆![]() 内切;②圆
内切;②圆![]() 与圆
与圆![]() 、
、![]() 都内切.利用椭圆的定义可求得轨迹
都内切.利用椭圆的定义可求得轨迹![]() 的方程;由直线
的方程;由直线![]() 与曲线
与曲线![]() 仅有三个公共点,可知直线
仅有三个公共点,可知直线![]() 与椭圆
与椭圆![]() 相切,对直线
相切,对直线![]() 的斜率是否存在进行分类讨论,联立直线
的斜率是否存在进行分类讨论,联立直线![]() 与椭圆
与椭圆![]() 的方程,利用弦长公式结合不等式的性质可求得
的方程,利用弦长公式结合不等式的性质可求得![]() 的最大值.
的最大值.
已知圆![]() ,
,![]() ,则圆
,则圆![]() 内含于圆
内含于圆![]() ,
,
圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ;圆
;圆![]() 的圆心为
的圆心为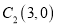 ,半径为
,半径为![]() .
.
设动圆![]() 的半径为
的半径为![]() ,分以下两种情况讨论:
,分以下两种情况讨论:
①圆![]() 与圆
与圆![]() 外切,与圆
外切,与圆![]() 内切,
内切,
由题意可得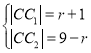 ,
,![]() ,
,
此时,圆![]() 的圆心轨迹
的圆心轨迹![]() 是以
是以![]() 、
、![]() 分别为左、右焦点,长轴长为
分别为左、右焦点,长轴长为![]() 的椭圆,
的椭圆,
![]() ,
,![]() ,则
,则![]() ,此时,轨迹
,此时,轨迹![]() 的方程为
的方程为![]() ;
;
②圆![]() 与圆
与圆![]() 、
、![]() 都内切,且
都内切,且![]() ,
,
由题意可得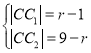 ,
,![]() ,
,
此时,圆![]() 的圆心轨迹
的圆心轨迹![]() 是以
是以![]() 、
、![]() 分别为左、右焦点,长轴长为
分别为左、右焦点,长轴长为![]() 的椭圆,
的椭圆,
![]() ,
,![]() ,
,![]() ,此时,轨迹
,此时,轨迹![]() 的方程为
的方程为![]() ;
;
综上所述,轨迹![]() 的方程为
的方程为![]() 或
或![]() ;
;
由于直线![]() 与曲线
与曲线![]() 仅有三个公共点,则直线
仅有三个公共点,则直线![]() 与椭圆
与椭圆![]() 相切.
相切.
①若直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
可设直线![]() 的方程为
的方程为![]() ,联立
,联立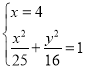 ,解得
,解得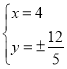 ,此时
,此时![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立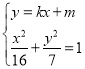 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,可得
,可得![]() ,
,
设点![]() 、
、![]() ,联立
,联立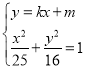 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
![]()
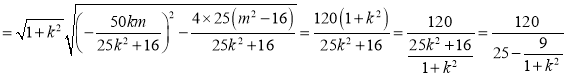 ,
,
![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
故答案为:![]() 或
或![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】
大学生是国家的未来,代表着国家可持续发展的实力,能够促进国家综合实力的提高.据统计,2016年至2020年我国高校毕业生人数y(单位:万人)的数据如下表:
年份 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代号x | 16 | 17 | 18 | 19 | 20 |
高校毕业生人数y(单位:万人) | 765 | 795 | 820 | 834 | 874 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性的强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测2022年我国高校毕业生的人数(结果取整数).
参考公式和数据: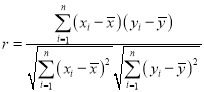 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)从该校学生中随机调查60名学生,一周参加社区服务时间超过1小时的人数记为X,以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,求X的分布列和数学期望.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 是椭圆与
是椭圆与![]() 轴负半轴的交点,经过
轴负半轴的交点,经过![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,经过
,经过![]() 且与
且与![]() 平行的直线与椭圆交于点
平行的直线与椭圆交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
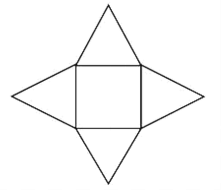
【题目】2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
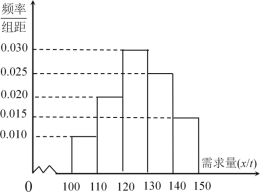
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com