

【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 是椭圆与
是椭圆与![]() 轴负半轴的交点,经过
轴负半轴的交点,经过![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,经过
,经过![]() 且与
且与![]() 平行的直线与椭圆交于点
平行的直线与椭圆交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】我国在北宋年间(公元1084年)第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.哈三中图书馆中正好有这十本书,现在小张同学从这十本书中任借三本阅读,那么他借到的三本书中书名中恰有一个“算”字的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 均相切,切点分别为
均相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于x的不等式
时,关于x的不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知某市穿城公路![]() 自西向东到达市中心
自西向东到达市中心![]() 后转向东北方向,
后转向东北方向,![]() ,现准备修建一条直线型高架公路
,现准备修建一条直线型高架公路![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,且要求市中心
,且要求市中心![]() 到
到![]() 所在的直线距离为
所在的直线距离为![]() .
.
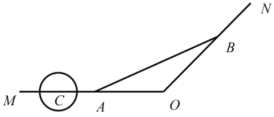
(1)求![]() ,
,![]() 两出入口间距离的最小值;
两出入口间距离的最小值;
(2)在公路![]() 段上距离市中心
段上距离市中心![]() 点
点![]() 处有一古建筑
处有一古建筑![]() (视为一点),现设立一个以
(视为一点),现设立一个以![]() 为圆心,
为圆心,![]() 为半径的圆形保护区,问如何在古建筑
为半径的圆形保护区,问如何在古建筑![]() 和市中心
和市中心![]() 之间设计出入口
之间设计出入口![]() ,才能使高架公路及其延长线不经过保护区?
,才能使高架公路及其延长线不经过保护区?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
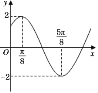
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在
,点E在![]() 上,且
上,且![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如图2).
(如图2).
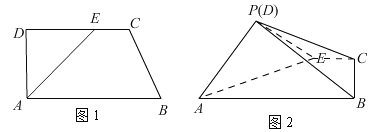
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点M,使
上是否存在点M,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点
,过点![]()
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() , 与椭圆交于另一个点
, 与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 且斜率大于
且斜率大于![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点(
两点(![]() ),若
),若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com