【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)函数![]() 在其定义域内有两个不同的极值点等价于方程
在其定义域内有两个不同的极值点等价于方程![]() 在
在![]() 有两个不同根,即函数
有两个不同根,即函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,讨论函数
上有两个不同交点,讨论函数![]() 单调性和极值根据图象即可求
单调性和极值根据图象即可求![]() 的取值范围;(2)作差得,
的取值范围;(2)作差得,![]() ,即
,即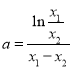 .原不等式
.原不等式![]() 等价于
等价于![]()
![]()
![]() ,
,![]() ,则
,则![]() ,只需证明不等式
,只需证明不等式![]() 成立即可.
成立即可.
试题解析:(1)依题意,函数![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有两个不同根.
有两个不同根.
即,方程![]() 在
在![]() 有两个不同根.
有两个不同根.
转化为,函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点.
上有两个不同交点.
又![]() ,即
,即![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,从而
上单调减,从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时,![]() ,在
,在![]() 时,
时,![]() ,
,
所以![]() 的草图如下,
的草图如下,
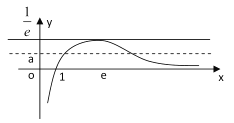
可见,要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() .
.
(2)由(1)可知![]() 分别是方程
分别是方程![]() 的两个根,即
的两个根,即![]() ,
,![]() ,
,
设![]() ,作差得,
,作差得,![]() ,即
,即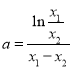 .
.
原不等式![]() 等价于
等价于
![]()
![]()
![]()
令![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即不等式![]() 成立,
成立,
故所证不等式![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
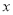 的方程
的方程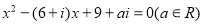 有实数根
有实数根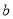 .
.(1)求实数
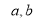 的值;
的值;(2)若复数
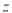 满足
满足 ,求
,求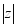 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
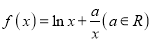 ,且函数
,且函数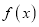 在
在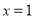 处的切线平行于直线
处的切线平行于直线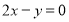 .
.(1)求实数
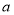 的值;
的值;(2)若在
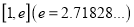 上存在一点
上存在一点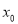 ,使得
,使得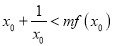 成立.求实数
成立.求实数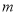 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解甲、乙两名同学的数学学习情况,对他们的
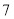 次数学测试成绩(满分
次数学测试成绩(满分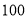 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是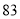 ,乙同学成绩的平均分是
,乙同学成绩的平均分是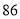 分.
分.(1)求
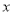 和
和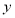 的值;
的值;(2)现从成绩在
 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.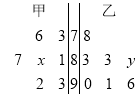
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x-
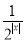 .
.(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b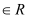 ,当
,当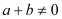 时,都有
时,都有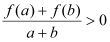 .
.(1)若
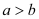 ,试比较
,试比较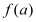 与
与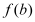 的大小关系;
的大小关系;(2)若
 对任意
对任意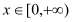 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润60元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(1)若商品一天购进该商品10件,求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量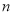 (单位:件,
(单位:件,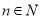 )的函数解析式;
)的函数解析式;(2)商店记录了50天该商品的日需求量
 (单位:件,
(单位:件, ),整理得下表:
),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间
 内的概率.
内的概率.
相关试题

