【题目】设![]() 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,试比较
,试比较![]() 与
与![]() 的大小关系;
的大小关系;
(2)若![]() 对任意
对任意![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)由![]() ,得
,得![]() ,所以f(a)+f(-b)>0,由f(x)是定义在R上的奇函数,能得到f(a)>f(b);(2)由f(x)在R上是单调递增函数,利用奇偶性、单调性可把
,所以f(a)+f(-b)>0,由f(x)是定义在R上的奇函数,能得到f(a)>f(b);(2)由f(x)在R上是单调递增函数,利用奇偶性、单调性可把![]() 中的符号“f”去掉,分离出参数k后转化为函数最值即可解决
中的符号“f”去掉,分离出参数k后转化为函数最值即可解决
试题解析:(1)因为![]() ,所以
,所以![]() ,由题意得:
,由题意得:
![]() ,所以
,所以![]() ,又
,又![]() 是定义在R上的奇函数,
是定义在R上的奇函数,
![]()
![]() ,
,
即![]() . ………6分
. ………6分
(2)由(1)知![]() 为R上的单调递增函数, ………7分
为R上的单调递增函数, ………7分
![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() ,
,
即![]() , ………9分
, ………9分
![]() ,
,![]() 对任意
对任意![]() 恒成立,
恒成立,
即k小于函数![]() 的最小值. ………11分
的最小值. ………11分
令![]() ,则
,则![]()
![]() ,
,
![]() . ………12分
. ………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解甲、乙两名同学的数学学习情况,对他们的
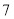 次数学测试成绩(满分
次数学测试成绩(满分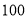 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是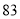 ,乙同学成绩的平均分是
,乙同学成绩的平均分是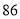 分.
分.(1)求
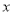 和
和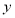 的值;
的值;(2)现从成绩在
 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.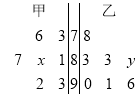
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.(1)求
 的取值范围;
的取值范围;(2)设两个极值点分别为
 ,证明:
,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x-
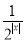 .
.(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润60元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(1)若商品一天购进该商品10件,求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量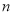 (单位:件,
(单位:件,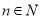 )的函数解析式;
)的函数解析式;(2)商店记录了50天该商品的日需求量
 (单位:件,
(单位:件, ),整理得下表:
),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间
 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
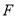 为抛物线
为抛物线 :
: 的焦点,点
的焦点,点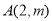 在抛物线
在抛物线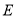 上,且到原点的距离为
上,且到原点的距离为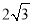 .
.(1)求抛物线
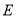 的方程;
的方程;(2)已知点
 ,延长
,延长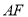 交抛物线
交抛物线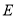 于点
于点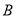 ,证明:以点
,证明:以点 为圆心且与直线
为圆心且与直线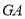 相切的圆,必与直线
相切的圆,必与直线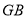 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】若有一个企业,70%的员工年收入1万元,25%的员工年收入3万元,5%的员工年收入11万元,则该企业员工的年收入的平均数是________万元,中位数是________万元,众数是________万元.
相关试题

