【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)根据椭圆几何条件得![]() ,又离心率为
,又离心率为![]() 得
得![]() ,解方程组得
,解方程组得![]() ,
,![]() ,
,
![]() (Ⅱ)先将向量条件坐标化,即由
(Ⅱ)先将向量条件坐标化,即由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,
再联立直线方程与椭圆方程,利用韦达定理化简得![]() ,
,
代入判别式大于零表达式化简得![]() 或
或![]() .
.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]()
![]() ,半焦距为
,半焦距为![]() . 依题意
. 依题意![]() ,由右焦点到右顶点的距离为
,由右焦点到右顶点的距离为![]() ,得
,得![]() .解得
.解得![]() ,
,![]() .所以
.所以![]() .
.
所以椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)解:存在直线![]() ,使得
,使得![]() 成立.理由如下:
成立.理由如下:
由 得
得![]() .
.
![]() ,化简得
,化简得![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
若![]() .所以
.所以![]() .
.![]() ,
,
![]() ,
,![]() ,
,
化简得,![]() .将
.将![]() 代入
代入![]() 中,
中,![]() ,
,
解得,![]() .又由
.又由![]() ,
,![]() ,
,
从而![]() ,
,![]() 或
或![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 中,
中, 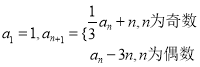 .
.(1)求证:数列
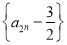 是等比数列;
是等比数列;(2)若是
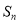 数列
数列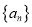 的前
的前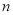 项和,求满足
项和,求满足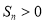 的所有正整数
的所有正整数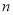 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】铁矿石A和B的含铁率为
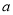 ,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石的价格c如下表:
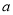
b(万吨)
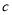 (百万元)
(百万元)A
50%
1
3
B
70%
0.5
6
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(改编)已知数列
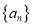 满足
满足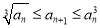 ,
, 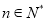 ,
, 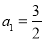 .
.(1)若
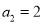 ,
,  ,
, 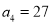 ,求实数
,求实数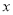 的取值范围;
的取值范围;(2)设数列
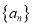 满足:
满足: 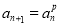 ,
, 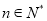 ,设
,设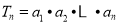 ,若
,若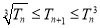 ,
, 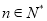 ,求
,求 的取值范围;
的取值范围;(3)若
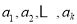 成公比
成公比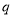 的等比数列,且
的等比数列,且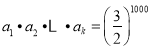 ,求正整数
,求正整数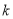 的最大值,以及
的最大值,以及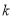 取最大值时相应数列
取最大值时相应数列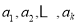 的公比
的公比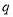 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
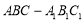 中,
中,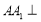 平面
平面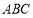 ,
,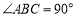 ,
,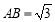 ,
,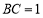 ,
,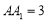 ,
,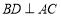 ,
,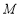 为线段
为线段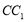 上一点.
上一点.(Ⅰ)求
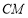 的值,使得
的值,使得 平面
平面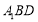 ;
;(Ⅱ)在(Ⅰ)的条件下,求二面角
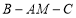 的正切值.
的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l、m 、n 与平面α、β给出下列四个命题:
①若m∥l,n∥l,则m∥n; ②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;④若m⊥β,α⊥β,则m∥α
其中,假命题的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场预计全年分批购入每台2000元的电视机共3600台.每批都购入
 台(
台( 是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
相关试题

