【题目】对于![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为-1的等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足
满足
![]() ?若存在,求出
?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“K数列”,数列
是“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,试判断数列
,试判断数列![]() 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)见解析.
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)由题意得![]() 和
和![]() ,即可求解实数
,即可求解实数![]() 的取值范围;
的取值范围;
(Ⅱ)设公差为![]() ,则
,则![]() ,得
,得![]() 对
对![]() 均成立,即
均成立,即![]() ,即可得到结论;
,即可得到结论;
(Ⅲ)设数列![]() 的公比为
的公比为![]() ,因为
,因为![]() 的每一项均为正整数,且
的每一项均为正整数,且![]() ,得到
,得到![]() ,且
,且![]() ,得到“
,得到“![]() ”和“
”和“![]() ”为最小项,又由又因为
”为最小项,又由又因为![]() 不是“K数列”, 且“
不是“K数列”, 且“![]() ”为最小项,得出
”为最小项,得出![]() ,所以
,所以![]() 或
或![]() ,分类讨论即可得到结论.
,分类讨论即可得到结论.
试题解析:(Ⅰ)由题意得![]() ,
,
![]() ,②
,②
解①得 ![]() ;
;
解②得 ![]() 或
或
所以![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)假设存在等差数列![]() 符合要求,设公差为
符合要求,设公差为![]() ,则
,则![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
由题意,得![]() 对
对![]() 均成立,
均成立,
即![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
因为![]() ,
,
所以![]() ,与
,与![]() 矛盾,
矛盾,
故这样的等差数列![]() 不存在.
不存在.
(Ⅲ)设数列![]() 的公比为
的公比为![]() ,则
,则![]() ,
,
因为![]() 的每一项均为正整数,且
的每一项均为正整数,且![]() ,
,
所以![]() ,且
,且![]() .
.
因为![]() ,
,
所以在![]() 中,“
中,“![]() ”为最小项.
”为最小项.
同理,在![]() 中,“
中,“![]() ”为最小项.
”为最小项.
由![]() 为“K数列”,只需
为“K数列”,只需![]() , 即
, 即 ![]() ,
,
又因为![]() 不是“K数列”, 且“
不是“K数列”, 且“![]() ”为最小项,所以
”为最小项,所以![]() , 即
, 即 ![]() ,
,
由数列![]() 的每一项均为正整数,可得
的每一项均为正整数,可得 ![]() ,
,
所以![]() 或
或![]() .
.
当![]() 时,
时,![]() , 则
, 则![]() ,
,
令![]() ,则
,则![]() ,
,
又![]()
![]() ,
,
所以![]() 为递增数列,即
为递增数列,即 ![]() ,
,
所以![]() .
.
因为![]() ,
,
所以对任意的![]() ,都有
,都有![]() ,
,
即数列![]() 为“K数列”.
为“K数列”.
当![]() 时,
时,![]() ,则
,则![]() .因为
.因为![]() ,
,
所以数列![]() 不是“K数列”.
不是“K数列”.
综上:当![]() 时,数列
时,数列![]() 为“K数列”,
为“K数列”,
当![]() 时,数列
时,数列![]() 不是“K数列” .
不是“K数列” .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn=n2+pn+q(p,q∈R),且a2 , a3 , a5成等比数列.
(1)求p,q的值;
(2)若数列{bn}满足an+log2n=log2bn , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|﹣1≤x≤2},B={x|x2﹣4x>0,x∈R},则A∩(RB)=( )
A.[1,2]
B.[0,2]
C.[1,4]
D.[0,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
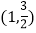 是椭圆E:
是椭圆E: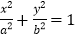 (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为 .
.(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
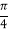 的直线与抛物线相交于A,B两点.
的直线与抛物线相交于A,B两点.(1)用p表示线段AB的长;
(2)若
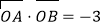 ,求这个抛物线的方程.
,求这个抛物线的方程.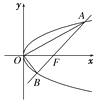
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个粮库要向A,B两镇运送大米,已知甲库可调出100 t大米,乙库可调出80 t大米,A镇需70 t大米,B镇需110 t大米.两库到两镇的路程和运费如下表:

这两个粮库各运往A,B两镇多少t大米,才能使总运费最省?此时总运费是多少?
相关试题

