【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)令![]() ,且函数
,且函数![]() 有三个彼此不相等的零点0,m,n,其中
有三个彼此不相等的零点0,m,n,其中![]() .
.
①若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②若对![]() ,
,![]() 恒成立,求实数t的去取值范围.
恒成立,求实数t的去取值范围.
参考答案:
【答案】(1)单调增区间是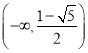 ,
,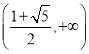 ;(2)①
;(2)①![]() ,②
,②![]() 或
或![]()
【解析】
(1)先求得函数![]() ,对函数
,对函数![]() 求导,令
求导,令![]() 大于零,解不等式即可求得单调增区间;
大于零,解不等式即可求得单调增区间;
(2)易知![]() ,
,![]() ,①求出
,①求出![]() ,
,![]() 的值,进而求得切线方程;②由对
的值,进而求得切线方程;②由对![]() ,
,![]() 恒成立,可得
恒成立,可得![]() ,分
,分![]() 与
与![]() 两种情况讨论,从而可求得
两种情况讨论,从而可求得![]() 的取值范围.
的取值范围.
(1)∵![]() ,
,![]()
∴![]()
∴![]() ,令
,令![]() ,得
,得![]() 或
或![]() .
.
∴![]() 的单调增区间是
的单调增区间是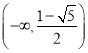 ,
,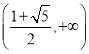 .
.
(2)由方程![]() ,得m,n是方程
,得m,n是方程![]() 的两实根,故
的两实根,故![]() ,
,![]() ,且由判别式得
,且由判别式得![]() .
.
①若![]() ,得
,得![]() ,
,![]() ,故
,故![]() ,得
,得![]() ,
,
因此![]() ,故函数
,故函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
②若对任意的![]() ,都有
,都有![]() 成立,所以
成立,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 时,对
时,对![]() 有
有![]() ,所以
,所以![]() ,解得
,解得![]() .又因为
.又因为![]() ,得
,得![]() ,则有
,则有![]() ;
;
当![]() 时,
时,![]() ,则存在
,则存在![]() 的极大值点
的极大值点![]() ,且
,且![]() .
.
由题意得![]() ,将
,将![]() 代入得
代入得![]() 进而得到
进而得到![]() ,得
,得![]() .
.
又因为![]() ,得
,得![]() .
.
综上可知t的取值范围是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正四棱锥
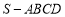 的底面边长为
的底面边长为 ,
,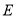 、
、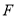 分别为
分别为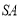 、
、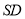 的中点.
的中点.
(1)当
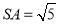 时,证明:平面
时,证明:平面 平面
平面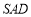 ;
;(2)若平面
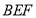 与底面
与底面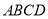 所成锐二面角为
所成锐二面角为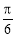 ,求直线
,求直线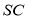 与平面
与平面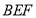 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
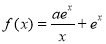 ,
,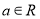 .
.(1)讨论
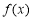 在区间
在区间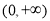 上的单调性;
上的单调性;(2)若
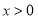 时,
时,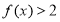 ,求整数
,求整数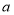 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:
 ,
,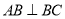 ,
,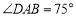 ,
,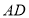 长1千米,
长1千米,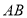 长
长 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊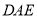 ,扇形
,扇形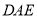 以
以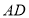 长为半径,弧
长为半径,弧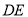 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段 线段
线段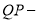 弧
弧 ,其中Q在线段
,其中Q在线段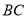 上(异于线段端点),
上(异于线段端点),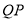 与弧
与弧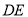 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情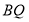 ,
,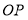 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧 的建造费用是每千米
的建造费用是每千米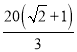 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设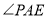 为
为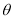 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为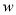 万元.
万元.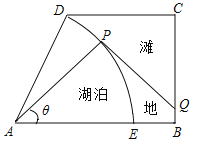
(1)求步行道的建造费用
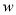 关于
关于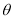 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;(2)当
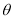 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
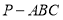 中,已知
中,已知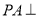 平面
平面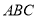 ,
,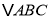 是边长为
是边长为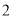 的正三角形,
的正三角形,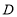 、
、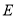 分别为
分别为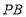 、
、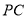 的中点.
的中点.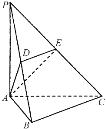
(1)若
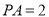 ,求直线
,求直线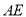 与
与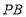 所成角的余弦值;
所成角的余弦值;(2)若平面
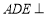 平面
平面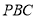 ,求
,求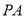 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记
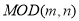 表示m除以n的余数,例如
表示m除以n的余数,例如 ,则输出i为( ).
,则输出i为( ).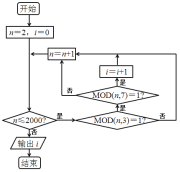
A.98B.97C.96D.95
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
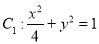 ,椭圆
,椭圆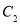 以
以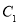 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆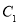 、
、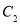 上,若
上,若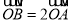 ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).A.1B.-1C.
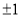 D.
D.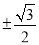
相关试题

