【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时, ![]() .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域.
参考答案:
【答案】
(1)解:∵f(x)在(﹣∞,0)∪(0,+∞)上是偶函数,
∴f(﹣x)=f(x)
设x<0,则﹣x>0,f(﹣x)=
∴
∴
(2)解:当x>0时, ,
令f'(x)=0x=2
∴当x∈(0,2)时,f'(x)<0,f(x)是减函数,
x∈(2,+∞)时,f'(0)>0,f(x)是增函数,
且函数f(x)在此区间上有极小值y极小=f(2)=5
又f(x)是偶函数,其图象关于y轴对称
∴x<0时,f(x)的增区间为(﹣2,0),减区间为(﹣∞,﹣2)
综上所述,f(x)在区间(﹣∞,﹣2)和(0,2)上是减函数
在区间(﹣2,0)和(2,+∞)上是增函数,值域为f(x)∈[5,+∞)
【解析】①先由奇偶性寻求f(﹣x)与f(x)的关系,再设x<0,则﹣x>0,按照求函数值求解;②用导数判断单调性,确定单调区间求得值域.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质和奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE:EB=1:2.
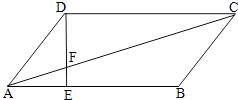
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O1和⊙O2的极坐标方程分别为ρ=4cosθ,ρ=﹣4sinθ.
(1)⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1和⊙O2交点的直线的直角坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=x2|x﹣a|(a∈R).21世纪教育网
(1)判定f(x)的奇偶性,并说明理由;
(2)当a≠0时,是否存在一点M(t,0),使f(x)的图象关于点M对称,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是
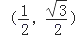 ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12] -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知.f(x)=sinxcosx-
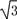 cos2x+
cos2x+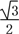
(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当0≤x≤
 时,求函数f(x)的值域.
时,求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.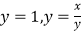
B.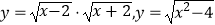
C.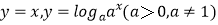
D.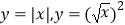
相关试题

