【题目】已知定义在R上的函数f(x)=x2|x﹣a|(a∈R).21世纪教育网
(1)判定f(x)的奇偶性,并说明理由;
(2)当a≠0时,是否存在一点M(t,0),使f(x)的图象关于点M对称,并说明理由.
参考答案:
【答案】
(1)解: a=0时,f(x)为偶函数;a≠0时,f(x)为非奇非偶函数.
(2)解:不存在.
假设存在一点M0(t0,0)使f(x)的图象关于点M对称,
则对x∈R应恒有f(t0+x)=﹣f(t0﹣x).
当t0=a时,取x=a,
则f(2a)=﹣f(0)=0,∴4a2|a|=0,∴a=0这与a≠0矛盾.当t0≠a时,
取x=a﹣t0,
则f(a)=﹣f(2t0﹣a)=0.∴(2t0﹣a)2|2t0﹣2a|=0,∵2t0﹣2a≠0,∴ .而 时,取x=0,
则 即 .∴ 这也与已知矛盾.
综上,不存在这样的点M.
【解析】分析:(1)根据f(x)=x2|x﹣a|(a∈R),可对a分类讨论,根据函数奇偶性的定义即可判断;(2)可假设存在一点M(t0 , 0)使f(x)的图象关于点M对称,故f(t0+x)=﹣f(t0﹣x);分当t0=a时,取x=a,有f(2a)=﹣f(0)=0,从而可得a=0,导出矛盾;
当t0≠a时,取x=a﹣t0 , f(a)=﹣f(2t0﹣a)=0,可解得 ![]() ,再取x=0,从而可得a=0,导出矛盾;于是可得结论.
,再取x=0,从而可得a=0,导出矛盾;于是可得结论.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE:EB=1:2.
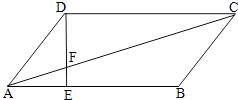
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O1和⊙O2的极坐标方程分别为ρ=4cosθ,ρ=﹣4sinθ.
(1)⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1和⊙O2交点的直线的直角坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时,
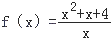 .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是
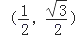 ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12] -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知.f(x)=sinxcosx-
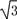 cos2x+
cos2x+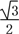
(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当0≤x≤
 时,求函数f(x)的值域.
时,求函数f(x)的值域.
相关试题

