【题目】如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD;
CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD;
(Ⅰ)求证:平面PAD⊥平面PCD;
(Ⅱ)若E是PC的中点.求三棱锥A﹣PEB的体积.
参考答案:
【答案】(Ⅰ)证明:∵PD⊥底面ABCD,∴PD⊥AD.
又由于CP∥AB,CP⊥CB,AB=BC
∴正方形ABCD,∴AD⊥CD,
又PD∩CD=D,故AD⊥底面PCD,
∵AD平面PAD,∴PAD⊥底面PCD
(Ⅱ)解:∵AD∥BC,BC平面PBC,AD平面PBC,∴AD∥平面PBC
∴点A到平面PBC的距离即为点D到平面PBC的距离
又∵PD=DC,E是PC的中点
∴PC⊥DE
由(Ⅰ)知有AD⊥底面PCD,∴有AD⊥DE.
由题意得AD∥BC,故BC⊥DE.
又∵PC∩BC=C
∴DE⊥面PBC.
∴ ![]() ,
, ![]() ,
,
又∵AD⊥底面PCD,∴AD⊥CP,
∵AD∥BC,∴AD⊥BC
∴ ![]()
∴ ![]()
【解析】(1)证明面面垂直找线面垂直,证明线面垂直找线线垂直。即PD⊥AD,AD⊥CD证明结论。
(2)证明点A到平面PBC的距离即为点D到平面PBC的距离,利用等体积转化法即可求出结论。
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上.

(1)AD边所在直线的方程;
(2)矩形ABCD外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程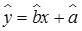 .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求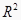 并说明模型的拟合效果.
并说明模型的拟合效果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的前n项和为Sn=a2n+b,且a1=3.
(1)求a、b的值及数列{an}的通项公式;
(2)设bn=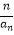 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)设各项均为正数的等比数列
 中,
中,

(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求证:
,求证:  ;
;(3)是否存在正整数
 ,使得
,使得 对任意正整数
对任意正整数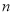 均成立?若存在,求出
均成立?若存在,求出 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲船在岛
 的正南方
的正南方 处,
处, 千米,甲船以每小时
千米,甲船以每小时 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自 出发以每小时
出发以每小时 千米的速度向北偏东
千米的速度向北偏东 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )A.
 分钟 B.
分钟 B.  分钟 C.
分钟 C.  分钟 D.
分钟 D.  分钟
分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ,
,  )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
相关试题

