【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.

(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
参考答案:
【答案】(1)255;(2)![]() ;(3)选择方案②获利多
;(3)选择方案②获利多
【解析】
1)由频率分布直方图能求出这组数据的平均数.(2)利用分层抽样从这两个范围内抽取5个芒果,则质量在[200,250)内的芒果有2个,记为a1,a2,质量在[250,300)内的芒果有3个,记为b1,b2,b3,从抽取的5个芒果中抽取2个,利用列举法能求出这2个芒果都来自同一个质量区间的概率.(3)方案①收入![]() 22950元,方案②:低于250克的芒果的收入为8400元,不低于250克的芒果的收入为17400元,由此能求出选择方案②获利多.
22950元,方案②:低于250克的芒果的收入为8400元,不低于250克的芒果的收入为17400元,由此能求出选择方案②获利多.
(1)由频率分布直方图知,各区间频率为0.07,0.15,0.20,0.30,0.25,0.03
这组数据的平均数
![]() .
.
(2)利用分层抽样从这两个范围内抽取5个芒果,则质量在[200,250)内的芒果有2个,记为![]() ,
,![]() ,质量在[250,300)内的芒果有3个,记为
,质量在[250,300)内的芒果有3个,记为![]() ,
,![]() ,
,![]() ;
;
从抽取的5个芒果中抽取2个共有10种不同情况:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
记事件![]() 为“这2个芒果都来自同一个质量区间”,则
为“这2个芒果都来自同一个质量区间”,则![]() 有4种不同组合:
有4种不同组合:
![]() ,
,![]() ,
,![]() ,
,![]()
从而![]() ,故这2个芒果都来自同一个质量区间的概率为
,故这2个芒果都来自同一个质量区间的概率为![]() .
.
(3)方案①收入:![]() (元);
(元);
方案②:低于250克的芒果收入为![]() (元);
(元);
不低于250克的芒果收入为![]() (元);
(元);
故方案②的收入为![]() (元).
(元).
由于![]() ,所以选择方案②获利多.
,所以选择方案②获利多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的普通方程和
的普通方程和 的直角坐标方程;
的直角坐标方程;(2)若
 与
与 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
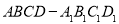 的底面
的底面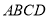 是菱形,
是菱形,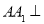 平面
平面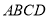 ,
,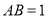 ,
,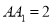 ,
,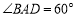 ,点
,点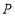 为
为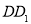 的中点.
的中点.
(1)求证:直线
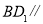 平面
平面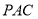 ;
;(2)求证:
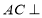 平面
平面 ;
;(3)求直线
 与平面
与平面 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.

(1)求直线PC与平面ABC所成角的大小;
(2)求二面角B﹣AP﹣C的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且a2an=S2+Sn对一切正整数n都成立.
(1)求a1 , a2的值;
(2)设a1>0,数列{lg }的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值.
}的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点M到两定点A(﹣1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.

(1)求轨迹C的方程;
(2)设直线y=﹣2x+m与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线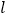 的参数方程为
的参数方程为 (
( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求直线
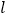 的普通方程及曲线
的普通方程及曲线 的直角坐标方程;
的直角坐标方程;(2)若直线
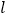 与曲线
与曲线 交于
交于 ,
, 两点,求
两点,求 .
.
相关试题

