【题目】如图,四棱柱![]() 的底面
的底面![]() 是菱形,
是菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成的角的正切值.
所成的角的正切值.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)只需证明PO∥BD1,即可得BD1∥平面PAC;(2)只需证明AC⊥BD.DD1⊥AC.即可证明AC⊥平面BDD1B1(3)∠CPO就是直线CP与平面BDD1B1所成的角,在Rt△CPO中,tan∠CPO![]() 即可求解
即可求解
(1)设![]() 和
和![]() 交于点
交于点![]() ,连结
,连结![]() ,
,
由于![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,故
的中点,故![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以直线![]() 平面
平面![]() .
.
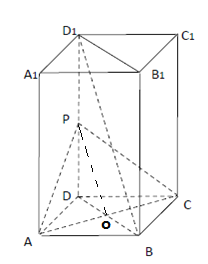
(2)在四棱柱![]() 中,
中,
底面![]() 是菱形,则
是菱形,则![]()
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
∴![]() 平面
平面![]() .
.
(3)由(2)知![]() 平面
平面![]() .
.
∴![]() 在平面
在平面![]() 内的射影为
内的射影为![]()
∴![]() 是
是![]() 与平面
与平面![]() 所成的角
所成的角
因为![]() ,所以
,所以![]() 为正三角形
为正三角形
∴![]()
![]() ,
,
在![]() 中,
中,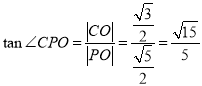 .
.
∴![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调区间;
的单调区间;(2)若函数
 在
在 处取得极值,对
处取得极值,对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了
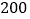 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在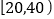 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表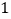 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
表:设备改造后样本的频数分布表
质量指标值
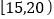
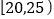
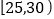
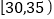
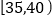
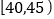
频数
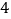
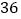
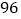
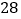
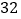
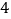
(1)完成下面的
 列联表,并判断是否有
列联表,并判断是否有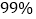 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;设备改造前
设备改造后
合计
合格品
不合格品
合计
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在
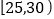 内的定为一等品,每件售价
内的定为一等品,每件售价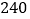 元;质量指标值落在
元;质量指标值落在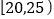 或
或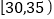 内的定为二等品,每件售价
内的定为二等品,每件售价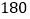 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价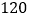 元.根据表
元.根据表 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为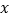 (单位:元),求
(单位:元),求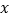 的分布列和数学期望.
的分布列和数学期望.附:
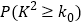
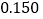
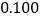
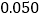
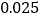

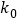
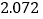
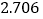
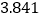
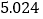

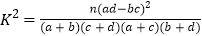
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的普通方程和
的普通方程和 的直角坐标方程;
的直角坐标方程;(2)若
 与
与 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.

(1)求直线PC与平面ABC所成角的大小;
(2)求二面角B﹣AP﹣C的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
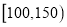 ,
, ,
, ,
, ,
, ,
, (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且a2an=S2+Sn对一切正整数n都成立.
(1)求a1 , a2的值;
(2)设a1>0,数列{lg }的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值.
}的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值.
相关试题

