搜索
【题目】（Ⅰ）抛物线的顶点在原点，坐标轴为对称轴，并经过点
，求此抛物线的方程.
（Ⅱ）已知圆： 
（
），把圆上的各点纵坐标不变，横坐标伸长到原来的
倍得一椭圆.求椭圆方程，并证明椭圆离心率是与
无关的常数.
参考答案：
【答案】（1）
或
（2）
【解析】试题分析：（1）根据题意设出抛物线的标准方程，注意两种形式，把点坐标代入即可；（2）利用图像的伸缩变换得到椭圆方程，计算椭圆离心率是一常数，故与c无关．
试题解析：（Ⅰ）依题意，若焦点在
轴，设抛物线的方程为
（
）
将
代入， 
，得
，此时方程为： 
若焦点在
轴，设抛物线的方程为
（
）
将
代入， 
，得
，此时方程为： 
所以，所求抛物线的方程为
或
（Ⅱ）设
是圆： 
上任一点，则
为所求椭圆上经过变换后的对应点，
则有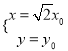
，即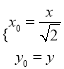
代入圆的方程得： 
．
故所求的椭圆方程为： 
．
又椭圆的长半轴的长为
，半焦距为
，故离心率
与
无关．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方形
与直角梯形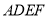
所在平面互相垂直， 
， 
， 
．
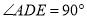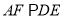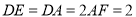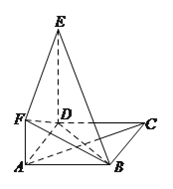
（I）求证：
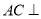平面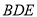
．（II）求证：
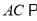平面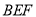
．（III）求四面体
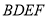的体积． -
科目： 来源： 题型：
查看答案和解析>>【题目】某钢厂打算租用
， 
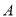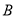两种型号的火车车皮运输900吨钢材， 
， 
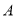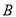两种车皮的载货量分别为36吨和60吨，租金分别为1.6万元/个和2.4万元/个，钢厂要求租车皮总数不超过21个，且
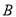型车皮不多于
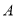型车皮7个，分别用
， 
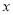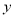表示租用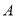
， 
两种车皮的个数.（Ⅰ）用
， 
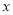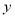列出满足条件的数学关系式，并画出相应的平面区域；（Ⅱ）分别租用
， 
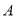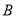两种车皮的个数是多少时，才能使得租金最少？并求出此最小租金. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正三棱柱
所有棱长都是2，D棱AC的中点，E是
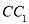棱的中点，AE交
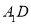于点H.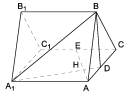
（1）求证：
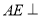平面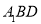
；（2）求二面角
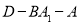的余弦值；（3）求点
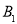到平面
的距离. -
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解高三学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出如图所示的频率分布直方图，已知从左到右各长方形高的比为2：3：5：6：3：1，则该班学生数学成绩在[100，120]之间的学生人数是（ ）
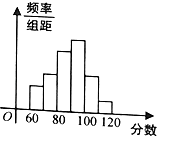
A.32
B.24
C.18
D.12 -
科目： 来源： 题型：
查看答案和解析>>【题目】根据如图给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）
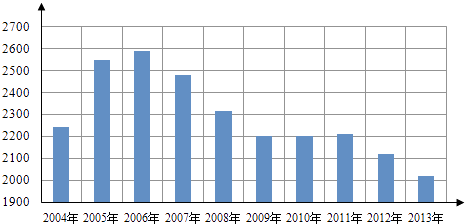
A.逐年比较，2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=cos4x﹣sin4x．下列结论正确的是（ ）
A.函数f（x）在区间[0，
]上是减函数
B.函数f（x）的图象关于原点对称
C.f（x）的最小正周期为
D.f（x）的值域为[﹣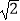
， ]
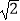相关试题
