【题目】某钢厂打算租用![]() ,
, ![]() 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材, ![]() ,
, ![]() 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且![]() 型车皮不多于
型车皮不多于![]() 型车皮7个,分别用
型车皮7个,分别用![]() ,
, ![]() 表示租用
表示租用![]() ,
, ![]() 两种车皮的个数.
两种车皮的个数.
(Ⅰ)用![]() ,
, ![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)分别租用![]() ,
, ![]() 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
参考答案:
【答案】(Ⅰ)见解析; (Ⅱ)分别租用![]() 、
、![]() 两种车皮5个,12个时租金最小,且最小租金为36.8万.
两种车皮5个,12个时租金最小,且最小租金为36.8万.
【解析】试题分析:
(Ⅰ)由已知条件列出![]() 的约束条件,可画出可行域;
的约束条件,可画出可行域;
(Ⅱ)求出目标函数为![]() ,作直线
,作直线![]() ,易知向上平移直线
,易知向上平移直线![]() 时,
时, ![]() 增大,从而可得最优解.
增大,从而可得最优解.
试题解析:
(Ⅰ)由已知![]() ,
, ![]() 满足的数学关系式为
满足的数学关系式为

该二元一次不等式组所表示的平面区域为图中阴影部分所示.
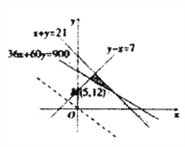
(Ⅱ)设租金为![]() 元,则目标函数
元,则目标函数![]() ,所以
,所以![]() ,这是斜率为
,这是斜率为![]() .在
.在![]() 轴上的截距为
轴上的截距为![]() 的一族平行直线.
的一族平行直线.
当![]() 取最小值时,
取最小值时, ![]() 的值最小,又因为
的值最小,又因为![]() ,
, ![]() 满足约束条件,所以由图可知,当直线
满足约束条件,所以由图可知,当直线![]() 经过可行域中的点
经过可行域中的点![]() 时,截距
时,截距![]() 的值最小,即
的值最小,即![]() 的值最小.
的值最小.
解方程组![]() ,得点
,得点![]() 的坐标为
的坐标为![]() .
.
所以![]() (万元).
(万元).
答:分别租用![]() 、
、![]() 两种车皮5个,12个时租金最小,且最小租金为36.8万.
两种车皮5个,12个时租金最小,且最小租金为36.8万.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
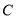 :
: 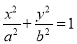 (
(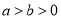 )与
)与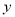 轴交于
轴交于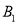 ,
, 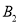 两点,
两点, 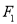 为椭圆
为椭圆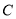 的左焦点,且
的左焦点,且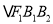 是边长为2的等边三角形.
是边长为2的等边三角形.(Ⅰ)求椭圆
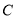 的方程;
的方程;(Ⅱ)设直线
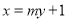 与椭圆
与椭圆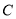 交于
交于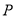 ,
, 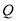 两点,点
两点,点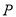 关于
关于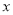 轴的对称点为
轴的对称点为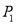 (
(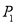 与
与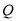 不重合),则直线
不重合),则直线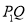 与
与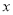 轴交于点
轴交于点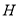 ,求
,求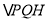 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
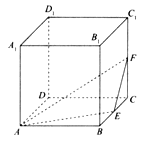
查看答案和解析>>【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
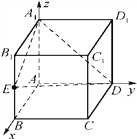
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形
 与直角梯形
与直角梯形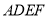 所在平面互相垂直,
所在平面互相垂直, 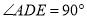 ,
, 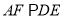 ,
, 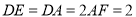 .
.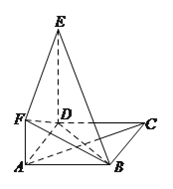
(I)求证:
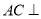 平面
平面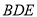 .
.(II)求证:
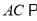 平面
平面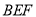 .
.(III)求四面体
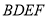 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱
 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是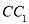 棱的中点,AE交
棱的中点,AE交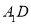 于点H.
于点H.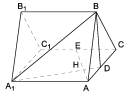
(1)求证:
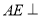 平面
平面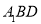 ;
;(2)求二面角
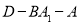 的余弦值;
的余弦值;(3)求点
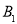 到平面
到平面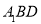 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)抛物线的顶点在原点,坐标轴为对称轴,并经过点
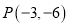 ,求此抛物线的方程.
,求此抛物线的方程.(Ⅱ)已知圆:
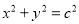 (
(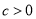 ),把圆上的各点纵坐标不变,横坐标伸长到原来的
),把圆上的各点纵坐标不变,横坐标伸长到原来的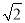 倍得一椭圆.求椭圆方程,并证明椭圆离心率是与
倍得一椭圆.求椭圆方程,并证明椭圆离心率是与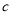 无关的常数.
无关的常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( )
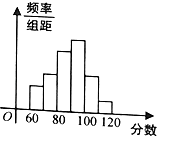
A.32
B.24
C.18
D.12
相关试题

