【题目】已知直线l在x轴上的截距比在y轴上的截距大1,且过点(6,-2),求直线l的方程.
参考答案:
【答案】y=-![]() x+2或y=-
x+2或y=-![]() x+1.
x+1.
【解析】试题分析:根据题干条件知道过点(6,-2),可设直线l的点斜式方程为y+2=k(x-6),分别求出直线的截距,在x轴上的截距比在y轴上的截距大1,故得![]() -(-6k-2)=1,从而求出k值。
-(-6k-2)=1,从而求出k值。
方法一:设直线l的点斜式方程为y+2=k(x-6)(k≠0).
令x=0,得y=-6k-2;令y=0,
得x=![]() +6.
+6.
于是![]() -(-6k-2)=1,
-(-6k-2)=1,
解得k1=-![]() 或k2=-
或k2=-![]() .
.
故直线l的方程为y+2=-![]() (x-6)或y+2=-
(x-6)或y+2=-![]() (x-6),即y=-
(x-6),即y=-![]() x+2或y=-
x+2或y=-![]() x+1.
x+1.
方法二:设直线l的斜截式方程为y=kx+b.
令y=0,得x=-![]() .
.
依题意,得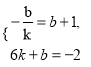
 或
或
故直线l的方程为y=-![]() x+1或y=-
x+1或y=-![]() x+2.
x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.
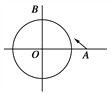
问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
-
科目: 来源: 题型:
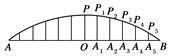
查看答案和解析>>【题目】某圆拱桥的示意图如图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了适应市场需要,某地准备建一个圆形生猪储备基地(如右图),它的附近有一条公路,从基地中心O处向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B;从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,求DE的最短距离.
-
科目: 来源: 题型:
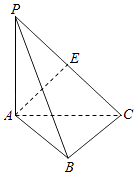
查看答案和解析>>【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足
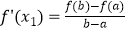 ,
, 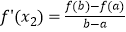 ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.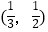
B.(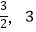 )
)
C.( ,1)
,1)
D.( ,1)
,1)
相关试题

