【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列2×2列联表,并回答能否有90%的把握认为年龄层与热衷关心民生大事有关?

(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?

![]() .
.
参考答案:
【答案】(1)青年观众为18人,中年观众12人;(2)见解析;(3)![]()
【解析】
(1)利用分层抽样原理计算抽出的人数即可;
(2)填写列联表,计算观测值,对照临界值得出结论;
(3)用列举法求基本事件数,计算所求的概率值.
(1)抽出的青年观众为18人,中年观众12人;
(2)2×2列联表如下:
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 6 | 12 | 18 |
中年 | 7 | 5 | 12 |
总计 | 13 | 17 | 30 |
计算观测值![]() ,
,
∴没有90%的把握认为年龄层与热衷关心民生大事有关;
(3)热衷关心民生大事的青年观众有6人,记能胜任才艺表演的四人为![]() ,
,
其余两人记为![]() ,则从中选两人,可得
,则从中选两人,可得![]()
![]()
共有如下15种情况,
抽出的2人都能胜任才艺表演的有![]() ,共有6种情况,
,共有6种情况,
所以所求的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a=7,b=8,cosB= –
 .
.(Ⅰ)求∠A;
(Ⅱ)求AC边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以平面直角坐标系
 的原点为极点,
的原点为极点,  轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线 的参数方程为
的参数方程为 (
( 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为 .
. (1)求直线
 的普通方程与圆
的普通方程与圆 的直角坐标方程;
的直角坐标方程; (2)设曲线
 与直线
与直线 交于
交于 两点,若
两点,若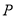 点的直角坐标为
点的直角坐标为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)证明:
 ;
;(2)证明:对任何正整数n,存在多项式函数
 ,使得
,使得 对所有实数x均成立,其中
对所有实数x均成立,其中 均为整数,当n为奇数时,
均为整数,当n为奇数时, ,当n为偶数时,
,当n为偶数时, ;
;(3)利用(2)的结论判断
 是否为有理数?
是否为有理数? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值
所成角的正切值 构成的集合是( )
构成的集合是( )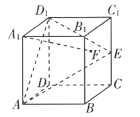
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推导球的体积公式,刘徽制造了一个牟合方盖(在一个正方体内作两个互相垂直的内切圆柱,这两个圆柱的公共部分叫做牟合方盖),但没有得到牟合方盖的体积.200年后,祖暅给出牟合方盖的体积计算方法,其核心过程被后人称为祖暅原理:缘幂势既同,则积不容异.意思是,夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截,如果截面的面积总相等,那么这两个几何体的体积也相等.现在截取牟合方盖的八分之一,它的外切正方体
 的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,下列结论中错误的是
,下列结论中错误的是A.

 , f(
, f( )=0
)=0B. 函数y=f(x)的图像是中心对称图形
C. 若
 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞, )单调递减
)单调递减D. 若
 是f(x)的极值点,则
是f(x)的极值点,则 (
( )=0
)=0
相关试题

