【题目】钝角三角形ABC的面积是 ![]() ,AB=1,BC=
,AB=1,BC= ![]() ,则AC=( )
,则AC=( )
A.5
B.![]()
C.2
D.1
参考答案:
【答案】B
【解析】解:∵钝角三角形ABC的面积是 ![]() ,AB=c=1,BC=a=
,AB=c=1,BC=a= ![]() ,
,
∴S= ![]() acsinB=
acsinB= ![]() ,即sinB=
,即sinB= ![]() ,
,
当B为钝角时,cosB=﹣ ![]() =﹣
=﹣ ![]() ,
,
利用余弦定理得:AC2=AB2+BC2﹣2ABBCcosB=1+2+2=5,即AC= ![]() ,
,
当B为锐角时,cosB= ![]() =
= ![]() ,
,
利用余弦定理得:AC2=AB2+BC2﹣2ABBCcosB=1+2﹣2=1,即AC=1,
此时AB2+AC2=BC2 , 即△ABC为直角三角形,不合题意,舍去,
则AC= ![]() .
.
故选:B.
利用三角形面积公式列出关系式,将已知面积,AB,BC的值代入求出sinB的值,分两种情况考虑:当B为钝角时;当B为锐角时,利用同角三角函数间的基本关系求出cosB的值,利用余弦定理求出AC的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了检测某种产品的质量(单位:千克),抽取了一个容量为N的样本,整理得到的数据作出了频率分布表和频率分布直方图如图:
分组
频数
频率
[17.5,20)
10
0.05
[20,225)
50
0.25
[22.5,25)
a
b
[25,27.5)
40
c
[27.5,30]
20
0.10
合计
N
1
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求频率分布直方图中d的值;
(Ⅲ)从该产品中随机抽取一件,试估计这件产品的质量少于25千克的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 =1(a>b>0)的左右焦点分别为F1 , F2 , 点
=1(a>b>0)的左右焦点分别为F1 , F2 , 点 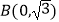 为短轴的一个端点,∠OF2B=60°.
为短轴的一个端点,∠OF2B=60°.
(Ⅰ)求椭圆C的方程;
(Ⅱ)如图,过右焦点F2 , 且斜率为k(k≠0)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线AE,AD分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.试问kk′是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=
 ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).(1)若数列{bn}满足bn=an-
 ,求证:{bn}是等比数列;
,求证:{bn}是等比数列;(2)求数列{an}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的个数是 ( )
①“x=
 ”是“
”是“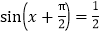 ”的充分不必要条件;
”的充分不必要条件;②若a>b,则am2>bm2;
③命题“x∈R,sinx≤1”的否定是“x∈R,sinx>1”;
④函数f(x)=
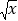 -cosx在[0,+∞)内有且仅有两个零点.
-cosx在[0,+∞)内有且仅有两个零点. A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知条件p:x2﹣3x﹣4≤0;条件q:x2﹣6x+9﹣m2≤0,若p是q的充分不必要条件,则m的取值范围是( )
A.[﹣1,1]
B.[﹣4,4]
C.(﹣∞,﹣1]∪[1,+∞)
D.(﹣∞,﹣4]∪[4,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
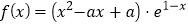 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)讨论函数
 的单调性;
的单调性;(3)若函数
 在
在 处取得极小值,设此时函数
处取得极小值,设此时函数 的极大值为
的极大值为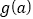 ,证明:
,证明: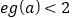 .
.
相关试题

