【题目】已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性。
的奇偶性。
参考答案:
【答案】(1){x|﹣1<x<1}(2)偶函数
【解析】
(1)要求函数f(x)+g(x)的定义域,我们可根据让函数解析式有意义的原则,构造不等式组,解不等式组即可得到函数f(x)+g(x)的定义域;
(2)要判断h(x)=f(x)+g(x)的奇偶性,我们根据奇偶性的定义,先判断其定义域是否关于原点对称,然后再判断f(﹣x)+g(﹣x)与f(x)+g(x)的关系,结合奇偶性的定义进行判断;
(1)f(x)+g(x)=![]() +
+![]() .
.
若要上式有意义,则![]() ,
,
即﹣1<x<1.
所以所求定义域为{x|﹣1<x<1}
(2)记h(x)=f(x)+g(x),定义域为{x|﹣1<x<1}
则h(﹣x)=f(﹣x)+g(﹣x)
=log2(﹣x+1)+log2(1+x)=h(x).
所以h(x)=f(x)+g(x)是偶函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-a)(x-b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 为增函数,且
为增函数,且 ,则
,则 等于( )
等于( )A.
 B.
B.  C.
C.  或
或 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为  ,上、下顶点分别是
,上、下顶点分别是  ,点
,点  是
是  的中点,若
的中点,若  ,且
,且  .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 的直线
的直线  与椭圆
与椭圆  交于不同的两点
交于不同的两点  ,求
,求  的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)若 ,讨论函数
,讨论函数  的单调性;
的单调性;
(2)曲线 与直线
与直线  交于
交于  ,
,  两点,其中
两点,其中  ,若直线
,若直线  斜率为
斜率为  ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线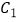 的极坐标方程是
的极坐标方程是 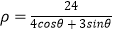 ,以极点为原点
,以极点为原点 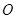 ,极轴为
,极轴为 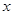 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 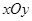 中,曲线
中,曲线 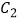 的参数方程为:
的参数方程为: 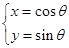 (
( 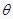 为参数).
为参数).
(1)求曲线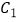 的直角坐标方程与曲线
的直角坐标方程与曲线 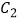 的普通方程;
的普通方程;
(2)将曲线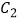 经过伸缩变换
经过伸缩变换 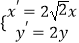 后得到曲线
后得到曲线 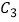 ,若
,若 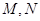 分别是曲线
分别是曲线 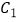 和曲线
和曲线 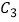 上的动点,求
上的动点,求  的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
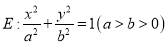 的离心率为
的离心率为 ,椭圆
,椭圆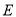 和抛物线
和抛物线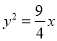 交于
交于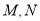 两点,且直线
两点,且直线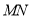 恰好通过椭圆
恰好通过椭圆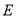 的右焦点
的右焦点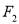 .
.(1)求椭圆
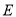 的标准方程;
的标准方程;(2)已知椭圆
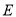 的左焦点为
的左焦点为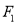 ,左、右顶点分别为
,左、右顶点分别为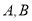 ,经过点
,经过点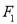 的直线
的直线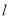 与椭圆
与椭圆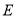 交于
交于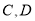 两点,记
两点,记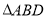 与
与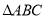 的面积分别为
的面积分别为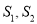 ,求
,求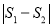 的最大值.
的最大值.
相关试题

