【题目】已知函数 ![]() .
.
(1)若 ![]() ,讨论函数
,讨论函数 ![]() 的单调性;
的单调性;
(2)曲线 ![]() 与直线
与直线 ![]() 交于
交于 ![]() ,
, ![]() 两点,其中
两点,其中 ![]() ,若直线
,若直线 ![]() 斜率为
斜率为 ![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】
(1)![]()
, ![]() ,当a≥0时,恒有
,当a≥0时,恒有 ![]() ,
, ![]() 在区间
在区间 ![]() 内是增函数;
内是增函数;
当a<0时,令 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,令
,令 ![]() 即
即 ![]() ,解得
,解得 ![]() ,综上,当a≥0时,
,综上,当a≥0时, ![]() 在区间
在区间 ![]() 内是增函数;
内是增函数;
当a<0时, ![]() 在
在 ![]() 内是增函数,在
内是增函数,在 ![]() 内是减函数.
内是减函数.
(2)
证明: ![]() ,要证明
,要证明 ![]() ,
,
即证 ![]() ,等价于
,等价于 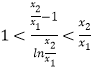 ,令
,令 ![]() (由
(由 ![]() ,知t>1),
,知t>1),
则只需证 ![]() ,由t>1,知
,由t>1,知 ![]() ,故等价于
,故等价于 ![]() (*)
(*)
①令 ![]() ,则
,则 ![]() ,所以
,所以 ![]() 在
在 ![]() 内是增函数,当t>1时,
内是增函数,当t>1时, ![]() ,所以
,所以 ![]() ;
;
②令 ![]() 则
则 ![]() ,所以
,所以 ![]() 在
在 ![]() 内是增函数,当t>1时,
内是增函数,当t>1时, ![]() ,即
,即 ![]() .
.
由①②知(*)成立,所以 ![]() .
.
【解析】本题考查利用导数求函数的单调性、极值、最值,函数与方程、不等式等基础知识,意在考查综合分析问题、解决问题的能力和基本运算能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 为增函数,且
为增函数,且 ,则
,则 等于( )
等于( )A.
 B.
B.  C.
C.  或
或 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为  ,上、下顶点分别是
,上、下顶点分别是  ,点
,点  是
是  的中点,若
的中点,若  ,且
,且  .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 的直线
的直线  与椭圆
与椭圆  交于不同的两点
交于不同的两点  ,求
,求  的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
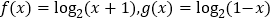
(1)求函数
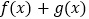 的定义域;
的定义域;(2)判断函数
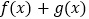 的奇偶性。
的奇偶性。 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线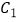 的极坐标方程是
的极坐标方程是 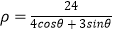 ,以极点为原点
,以极点为原点 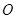 ,极轴为
,极轴为 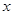 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 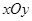 中,曲线
中,曲线 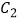 的参数方程为:
的参数方程为: 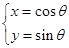 (
( 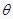 为参数).
为参数).
(1)求曲线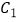 的直角坐标方程与曲线
的直角坐标方程与曲线 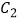 的普通方程;
的普通方程;
(2)将曲线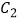 经过伸缩变换
经过伸缩变换 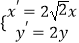 后得到曲线
后得到曲线 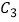 ,若
,若 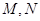 分别是曲线
分别是曲线 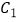 和曲线
和曲线 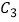 上的动点,求
上的动点,求  的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
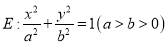 的离心率为
的离心率为 ,椭圆
,椭圆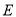 和抛物线
和抛物线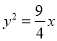 交于
交于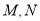 两点,且直线
两点,且直线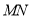 恰好通过椭圆
恰好通过椭圆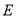 的右焦点
的右焦点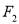 .
.(1)求椭圆
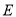 的标准方程;
的标准方程;(2)已知椭圆
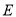 的左焦点为
的左焦点为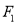 ,左、右顶点分别为
,左、右顶点分别为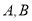 ,经过点
,经过点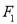 的直线
的直线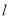 与椭圆
与椭圆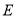 交于
交于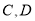 两点,记
两点,记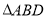 与
与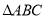 的面积分别为
的面积分别为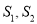 ,求
,求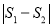 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0 , f(x0)),其中x0满足f″(x0)=0.已知f(x)=
 x3﹣
x3﹣  x2+3x﹣
x2+3x﹣  ,则f(
,则f( 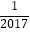 )+f(
)+f(  )+f(
)+f(  )+…+f(
)+…+f(  )=( )
)=( )
A.2013
B.2014
C.2015
D.2016
相关试题

