【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
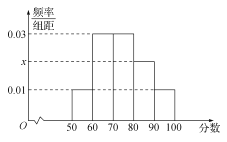
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
参考答案:
【答案】(1)![]() ,平均数是74,中位数是
,平均数是74,中位数是![]() ;(2)1200;(3)
;(2)1200;(3)![]() .
.
【解析】试题分析:(1)根据个矩形面积和为![]() 可得第4组的频率为
可得第4组的频率为![]() ,从而可得结果;(2)由(1)可知,50名学生中成绩不低于70分的频率为
,从而可得结果;(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,从而可得成绩不低于70分的人数;(3)根据分层抽样方法可得这三组中所抽取的人数分别为3,2,1,列举出中任抽取3人的所有可能结果共20种,其中后两组中没有人被抽到的可能结果只有1种,由古典概型概率公式可得结果.
,从而可得成绩不低于70分的人数;(3)根据分层抽样方法可得这三组中所抽取的人数分别为3,2,1,列举出中任抽取3人的所有可能结果共20种,其中后两组中没有人被抽到的可能结果只有1种,由古典概型概率公式可得结果.
(1)由频率分布直方图可得第4组的频率为![]()
![]() ,
,
故![]() .
.
故可估计所抽取的50名学生成绩的平均数为
![]()
![]()
![]() (分).
(分).
由于前两组的频率之和为![]() ,前三组的频率之和为
,前三组的频率之和为![]() ,故中位数在第3组中.
,故中位数在第3组中.
设中位数为![]() 分,
分,
则有![]() ,所以
,所以![]() ,
,
即所求的中位数为![]() 分.
分.
(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,
,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为![]() .
.
(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
,![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共20种.
共20种.
其中后两组中没有人被抽到的可能结果为![]() ,只有1种,
,只有1种,
故后两组中至少有1人被抽到的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
A.2,
B.4,3
C.4,
D.2,1 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个结论:
①若命题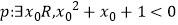 ,则p:x∈R,x2+x+1≥0;
,则p:x∈R,x2+x+1≥0;
②“(x﹣3)(x﹣4)=0”是“x﹣3=0”的充分而不必要条件;
③命题“若m>0,则方程x2+x﹣m=0有实数根”的逆否命题为:“若方程x2+x﹣m=0没有实数根,则m≤0”;
④若a>0,b>0,a+b=4,则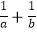 的最小值为1.
的最小值为1.
其中正确结论的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ),数列
),数列 的前
的前 项和为
项和为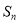 ,点
,点 在
在 图象上,且
图象上,且 的最小值为
的最小值为 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 满足
满足 ,记数列
,记数列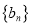 的前
的前 项和为
项和为 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R的函数f(x)=
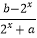 是奇函数,其中a,b为实数
是奇函数,其中a,b为实数
(1)求a,b的值
(2)用定义证明f(x)在R上是减函数
(3)若对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)在R上可导,其导函数为f′(x),若f(x)满足
 >0,f(2﹣x)=f(x)e2﹣2x则下列判断一定正确的是( )
>0,f(2﹣x)=f(x)e2﹣2x则下列判断一定正确的是( )
A.f(1)<f(0)
B.f(3)>e3f(0)
C.f(2)>ef(0)
D.f(4)<e4f(0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆 交于
交于 ,
,  两点.
两点.(1)求圆
 的直角坐标方程及弦
的直角坐标方程及弦 的长;
的长;(2)动点
 在圆
在圆 上(不与
上(不与 ,
,  重合),试求
重合),试求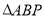 的面积的最大值.
的面积的最大值.
相关试题

