【题目】已知定义在R的函数f(x)= ![]() 是奇函数,其中a,b为实数
是奇函数,其中a,b为实数
(1)求a,b的值
(2)用定义证明f(x)在R上是减函数
(3)若对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,求k的取值范围.
参考答案:
【答案】
(1)解:∵函数f(x)= ![]() 是R上的奇函数,
是R上的奇函数,
∴f(0)= ![]() =0,∴b=1.
=0,∴b=1.
又f(1)+f(﹣1)= ![]() +
+ ![]() =0,解得:a=1,
=0,解得:a=1,
∴a=b=1
(2)解:由(1)知,f(x)= ![]() =﹣1+
=﹣1+ ![]() ,
,
令x1<x2,则 ![]() <
< ![]() ,
,
∴f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() >0,
>0,
∴f(x)在R上是减函数
(3)解:∵对于任意的t∈[﹣3,3],f(t2﹣2t)+f(﹣2t2+k)<0恒成立,f(x)= ![]() 为奇函数,
为奇函数,
∴f(t2﹣2t<﹣f(﹣2t2+k)=f(2t2﹣k),
又f(x)在R上是减函数.
∴t2﹣2t>2t2﹣k恒成立,t∈[﹣3,3].
∴k>(t2﹣2t)max,又y=t2﹣2t的对称轴方程为t=1,∴t=﹣3时,函数取得最大值,即ymax=15,
∴k>15,即k的取值范围为:(15,+∞)
【解析】(1)依题意,由f(0)=0可求得b,再由f(1)+f(﹣1)=0可求得a的值;(2)令x1<x2 , 作差f(x1)﹣f(x2)= ![]() 判定符号即可证明f(x)在R上是减函数;(3)对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,利用R上的奇函数f(x)单调递减的性质性可得t2﹣2t>2t2﹣k恒成立,t∈[﹣3,3],整理得k>(t2﹣2t)max , t∈[﹣3,3],从而可求k的取值范围.
判定符号即可证明f(x)在R上是减函数;(3)对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,利用R上的奇函数f(x)单调递减的性质性可得t2﹣2t>2t2﹣k恒成立,t∈[﹣3,3],整理得k>(t2﹣2t)max , t∈[﹣3,3],从而可求k的取值范围.
【考点精析】利用函数单调性的判断方法对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个结论:
①若命题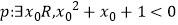 ,则p:x∈R,x2+x+1≥0;
,则p:x∈R,x2+x+1≥0;
②“(x﹣3)(x﹣4)=0”是“x﹣3=0”的充分而不必要条件;
③命题“若m>0,则方程x2+x﹣m=0有实数根”的逆否命题为:“若方程x2+x﹣m=0没有实数根,则m≤0”;
④若a>0,b>0,a+b=4,则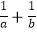 的最小值为1.
的最小值为1.
其中正确结论的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ),数列
),数列 的前
的前 项和为
项和为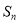 ,点
,点 在
在 图象上,且
图象上,且 的最小值为
的最小值为 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 满足
满足 ,记数列
,记数列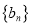 的前
的前 项和为
项和为 ,求证:
,求证:  .
. -
科目: 来源: 题型:
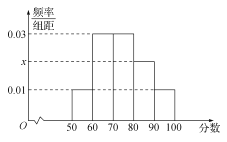
查看答案和解析>>【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为
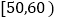 ,
,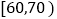 ,…,
,…,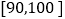 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).(1)求频率分布直方图中的
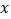 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)在R上可导,其导函数为f′(x),若f(x)满足
 >0,f(2﹣x)=f(x)e2﹣2x则下列判断一定正确的是( )
>0,f(2﹣x)=f(x)e2﹣2x则下列判断一定正确的是( )
A.f(1)<f(0)
B.f(3)>e3f(0)
C.f(2)>ef(0)
D.f(4)<e4f(0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆 交于
交于 ,
,  两点.
两点.(1)求圆
 的直角坐标方程及弦
的直角坐标方程及弦 的长;
的长;(2)动点
 在圆
在圆 上(不与
上(不与 ,
,  重合),试求
重合),试求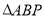 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x+
 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在  上是减函数,在
上是减函数,在  上是增函数.
上是增函数.
(1)已知f(x)= ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
相关试题

