【题目】 【2016高考新课标Ⅲ文数】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(I)若![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,证明
的中点,证明![]() ;
;
(II)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)设出与![]() 轴垂直的两条直线,然后得出
轴垂直的两条直线,然后得出![]() 的坐标,然后通过证明直线
的坐标,然后通过证明直线![]() 与直线
与直线![]() 的斜率相等即可证明结果了;(Ⅱ)设直线
的斜率相等即可证明结果了;(Ⅱ)设直线![]() 与
与![]() 轴的交点坐标
轴的交点坐标![]() ,利用面积可求得
,利用面积可求得![]() ,设出
,设出![]() 的中点
的中点![]() ,根据
,根据![]() 与
与![]() 轴是否垂直分两种情况结合
轴是否垂直分两种情况结合![]() 求解.
求解.
试题解析:由题设![]() .设
.设![]() ,则
,则![]() ,且
,且
![]() .
.
记过![]() 两点的直线为
两点的直线为![]() ,则
,则![]() 的方程为
的方程为![]() . .....3分
. .....3分
(Ⅰ)由于![]() 在线段
在线段![]() 上,故
上,故![]() .
.
记![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,则
,则![]() ,
,
所以![]() . ......5分
. ......5分
(Ⅱ)设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
则![]() .
.
由题设可得![]() ,所以
,所以![]() (舍去),
(舍去),![]() .
.
设满足条件的![]() 的中点为
的中点为![]() .
.
当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 可得
可得![]() .
.
而![]() ,所以
,所以![]() .
.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与
与![]() 重合,所以,所求轨迹方程为
重合,所以,所求轨迹方程为![]() . ....12分
. ....12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学(文)】已知双曲线
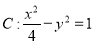 的左右两个顶点是
的左右两个顶点是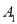 ,
, 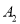 ,曲线
,曲线 上的动点
上的动点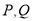 关于
关于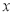 轴对称,直线
轴对称,直线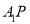 与
与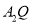 交于点
交于点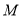 ,
,(1)求动点
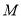 的轨迹
的轨迹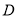 的方程;
的方程;(2)点
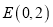 ,轨迹
,轨迹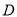 上的点
上的点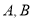 满足
满足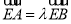 ,求实数
,求实数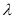 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考浙江文数】如图,设抛物线
 的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1. 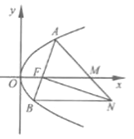
(I)求p的值;
(II)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x
轴交于点M.求M的横坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足:2a1+22a2+23a3+…+2nan=(n+1)2(n∈N*),则数列{an}的前n项和为 Sn= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和
项和 ,且
,且 是2与
是2与 的等差中项.
的等差中项.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知sin(x﹣
 )=
)= 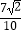 ,cos2x=
,cos2x= 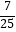 , (Ⅰ)求
, (Ⅰ)求 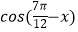 的值;
的值;
(Ⅱ)求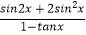 的值.
的值.
相关试题

