【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
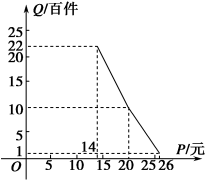
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
参考答案:
【答案】(1)商品的价格为每件19.5元时,月利润余额最大,为450元. (2) 20
【解析】
试题分析:(1)根据利润等于销售额乘以单价减去成本得:L=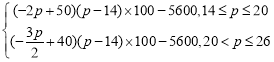 ,再分段根据二次函数对称轴与定义区间位置关系求最大值,最后取两个最大值中最大值(2) 由脱贫的含义:无债务,列不等式:12n×450-50 000-58 000≥0,解得n≥20.
,再分段根据二次函数对称轴与定义区间位置关系求最大值,最后取两个最大值中最大值(2) 由脱贫的含义:无债务,列不等式:12n×450-50 000-58 000≥0,解得n≥20.
试题解析:设该店月利润余额为L元,
则由题设得L=Q(P-14)×100-3 600-2 000,(*)
由销量图易得Q=
代入*式得L=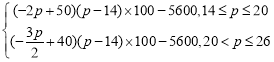
(1)当14≤P≤20时,Lmax=450元,此时P=19.5元;
当20<P≤26时,Lmax=![]() 元,此时P=
元,此时P=![]() 元.
元.
故当P=19.5元时,月利润余额最大,为450元.
(2)设可在n年后脱贫,
依题意有12n×450-50 000-58 000≥0,解得n≥20.
即最早可望在20年后脱贫.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为3的正三角形
 中,
中,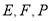 分别是
分别是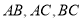 边上的点,满足
边上的点,满足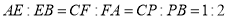 (如图
(如图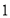 ),将
),将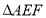 折起到
折起到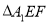 的位置上,连接
的位置上,连接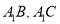 (如图).
(如图).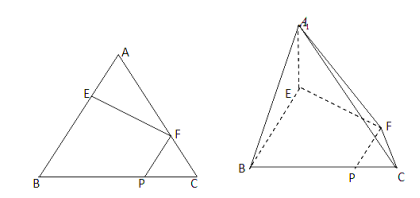
(1)在线段A1C上是否存在点Q,使得面QFP//面A1EB,证明你的结论;
(2)求证:
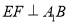 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.
(2)设直线l的方程为(a+1)x+y+2-a=0(a∈R).若l在两坐标轴上的截距相等,求l的方程;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题:“
 ,使等式
,使等式 成立”是真命题.
成立”是真命题.(1)求实数
 的取值集合
的取值集合 ;
;(2)设不等式
 的解集为
的解集为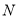 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的方程为
的方程为 ,点
,点 的坐标为
的坐标为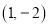 .
.(Ⅰ)求过
 点且与直线
点且与直线 平行的直线方程;
平行的直线方程;(Ⅱ)求过
 点且与直线
点且与直线 垂直的直线方程.
垂直的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用国庆节进行社会实践,对
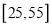 岁的人群随机抽取
岁的人群随机抽取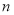 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:组数
分组
低碳族的人数
占本组的频率
第一组
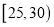
120
0.6
第二组

195
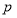
第三组
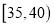
100
0.5
第四组
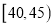
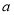
0.4
第五组
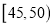
30
0.3
第六组

15
0.3
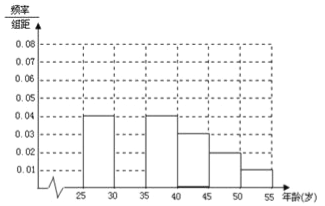
(1)补全频率分布直方图并求
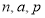 的值(直接写结果);
的值(直接写结果);(2)从年龄段在
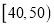 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在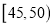 岁的概率.
岁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高一学生的数学与地理的水平测试成绩抽样统计如下表:若抽取的学生数为
 ,成绩分为
,成绩分为 (优秀)、
(优秀)、 (良好)、
(良好)、 (及格)三个等级,设
(及格)三个等级,设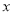 ,
,  分别表示数学成绩与地理成绩.例如:表中地理成绩为
分别表示数学成绩与地理成绩.例如:表中地理成绩为 等级的共有
等级的共有 人,数学成绩为
人,数学成绩为 级且地理成绩为
级且地理成绩为 等级的有8人.已知
等级的有8人.已知 与
与 均为
均为 等级的频率是0.07.
等级的频率是0.07.(1)设在该样本中,数学成绩优秀率是
 ,求
,求 ,
,  的值;
的值;(2)已知
 ,
,  ,求数学成绩为
,求数学成绩为 等级的人数比数学成绩为
等级的人数比数学成绩为 等级的人数多的概率.
等级的人数多的概率.
人数





14
40
10


36


28
8
34
相关试题

