【题目】已知函数![]() ,该函数图像过点
,该函数图像过点![]() ,与点
,与点![]() 相邻函数图像上的一个最高点为
相邻函数图像上的一个最高点为![]() .
.
(1)求该函数的解析式![]() ;
;
(2)求函数![]() 在区间
在区间![]() 上的最值及其对应的自变量
上的最值及其对应的自变量![]() 的值.
的值.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由已知可求T,利用周期公式可求ω,由函数经过点D的坐标为![]() ,可得
,可得![]() ,结合范围
,结合范围![]() ,即可得解函数的解析式;
,即可得解函数的解析式;
(2)利用正弦函数的性质可求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
试题解析:
(1)由题意得![]() 或
或![]() ,所以本题有两组解
,所以本题有两组解
①∴![]() ,又
,又![]() ,
,
∴![]() ,函数图象上最高点为
,函数图象上最高点为![]() ,
,
代入函数解析式得![]() ,
,
∵![]() ,∴
,∴![]()
∴函数的解析式为![]()
②∴![]() ,又
,又![]()
∴![]() ,函数图象上最高点为
,函数图象上最高点为![]() ,
,
代入函数解析式得![]() ,
,
∵![]() ,∴
,∴![]()
∴函数的解析式为![]()
(2)①![]() 时,
时, ![]() ,
,
∴![]() ,即
,即![]() 时,
时,
函数![]() 有最小值
有最小值![]()
![]() ,即
,即![]() 时,
时,
函数![]() 有最大值2
有最大值2
②![]() 时,
时, ![]() ,
,
∴![]() ,即
,即![]() 时,
时,
函数![]() 有最小值-2
有最小值-2
![]() 或
或![]() ,即
,即![]() 或
或![]() 时,
时,
函数![]() 有最大值2
有最大值2
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①球的半径是球面上任意一点与球心的连线;②球的直径是球面上任意两点的连线;③用一个平面截一个球面,得到的是一个圆;④球常用表示球心的字母表示.
其中说法正确的是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边
 中,
中, ,
, 分别为
分别为 ,
, 边的中点,
边的中点, 为
为 的中点,
的中点,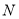 为
为 边上一点,且
边上一点,且 ,将
,将 沿
沿 折到
折到 的位置,使平面
的位置,使平面 平面
平面 .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知
 ,
, ,
, ,曲线
,曲线 是以点
是以点 为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在
为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段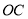 上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
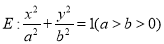 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.(Ⅰ)求椭圆
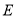 的方程;
的方程;(Ⅱ)若
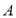 是椭圆
是椭圆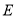 的左顶点,经过左焦点
的左顶点,经过左焦点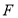 的直线
的直线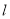 与椭圆
与椭圆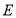 交于
交于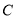 ,
,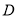 两点,求
两点,求 与
与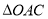 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(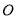 为坐标原点)
为坐标原点) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校对任课教师的年龄状况和接受教育程度(学历)做调研,其部分结果(人数分布)如表:
学历
35岁以下
35~50岁
50岁以上
本科
80
30
20
研究生
x
20
y
(1)用分层抽样的方法在35~50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人的学历为研究生的概率;
(2)若按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为
 ,求x、y的值.
,求x、y的值.
相关试题

