【题目】某学校对任课教师的年龄状况和接受教育程度(学历)做调研,其部分结果(人数分布)如表:
学历 | 35岁以下 | 35~50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(1)用分层抽样的方法在35~50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人的学历为研究生的概率;
(2)若按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为![]() ,求x、y的值.
,求x、y的值.
参考答案:
【答案】(1)![]() (2)x=40,y=5
(2)x=40,y=5
【解析】
试题分析:(1)由题意得:抽到35岁至50岁本科生3人,研究生2人,由此利用列举法能求出从中任取2人,至少有l人的学历为研究生的概率.(2)由题意得:![]() ,由此能求出N,从而能求出x,y的值
,由此能求出N,从而能求出x,y的值
试题解析:(1)用分层抽样的方法在35~50岁中抽取一个容量为5的样本,设抽取学历为本科的人数为m,∴![]() ,解得m=3.
,解得m=3.
∴抽取了学历为研究生的2人,学历为本科的3人,
分别记作S1、S2;B1、B2、B3.
从中任取2人的所有基本事件共10个:
(S1,B1),(S1,B2),(S1,B3),(S2,B1),(S2,B2),(S2,B3),(S1,S2),(B1,B2),
(B2,B3),(B1,B3).
其中至少有1人的学历为研究生的基本事件有7个:(S1,B1),(S1,B2),(S1,B3),
(S2,B1),(S2,B2),(S2,B3),(S1,S2).
∴从中任取2人,至少有1人的教育程度为研究生的概率为![]()
(2)依题意得:![]() ,解得N=78.
,解得N=78.
∴35~50岁中被抽取的人数为78-48-10=20.
∴ ![]() ,解得x=40,y=5.∴x=40,y=5.
,解得x=40,y=5.∴x=40,y=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,该函数图像过点
,该函数图像过点 ,与点
,与点 相邻函数图像上的一个最高点为
相邻函数图像上的一个最高点为 .
.(1)求该函数的解析式
 ;
;(2)求函数
 在区间
在区间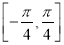 上的最值及其对应的自变量
上的最值及其对应的自变量 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知
 ,
, ,
, ,曲线
,曲线 是以点
是以点 为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在
为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段 上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
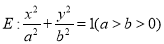 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若
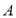 是椭圆
是椭圆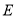 的左顶点,经过左焦点
的左顶点,经过左焦点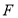 的直线
的直线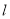 与椭圆
与椭圆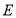 交于
交于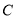 ,
,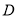 两点,求
两点,求 与
与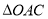 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(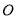 为坐标原点)
为坐标原点) -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
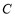 的极坐标方程为
的极坐标方程为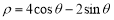 ,直线
,直线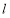 的参数方程为
的参数方程为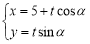 (
(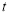 为参数).若直线
为参数).若直线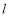 与圆
与圆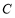 相交于不同的两点
相交于不同的两点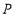 ,
,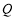 .
.(Ⅰ)写出圆
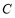 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长
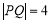 ,求直线
,求直线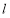 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:

(1)将上面表格中缺少的数据填在相应位置上;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的动直线
的动直线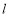 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点,  与直线
与直线 :
: 相交于
相交于 .
.
(1)当
 与
与 垂直时,求直线
垂直时,求直线 的方程,并判断圆心
的方程,并判断圆心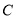 与直线
与直线 的位置关系;
的位置关系;(2)当
 时,求直线
时,求直线 的方程.
的方程.
相关试题

