搜索
【题目】《九章算术》是我国古代数学名著，也是古代东方数学的代表作．书中有如下问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“已知直角三角形两直角边长分别为5步和12步，问其内接正方形边长为多少步？”现若向此三角形内投豆子，则落在其内接正方形内的概率是（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：由题意，直角三角形两直角边长分别为5步和12步，面积为30，设内接正方形边长为x，则 
，解得x= 
，所以正方形 的面积为 
， ∴向此三角形内投豆子，则落在其内接正方形内的概率是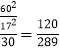 
，
故选：C．
【考点精析】利用几何概型对题目进行判断即可得到答案，需要熟知几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
为坐标原点，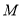 
是椭圆
上的点，设动点
满足
.（1）求动点
的轨迹
的方程；（2）若直线
与曲线
相交于
， 
两个不同点，求
面积的最大值. -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.命题“若x2=9，则x=±3”的否命题为“若x2=9，则x≠±3”
B.若命题P：?x0∈R，
，则命题?P：?x∈R， 
C.设
是两个非零向量，则“ 
是“ 夹角为钝角”的必要不充分条件
D.若命题P：
，则￢P： 
-
科目： 来源： 题型：
查看答案和解析>>【题目】为选拔选手参加“中国汉字听写大全”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．
（Ⅰ）求样本容量n和频率分布直方图中的x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“中国汉字听写大会”，每次抽取1人，求在第1次抽取的成绩低于90分的前提下，第2次抽取的成绩仍低于90分的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义在[0，+∞）上的函数f（x）满足f（x）=2f（x+2），当x∈[0，2）时，f（x）=﹣2x2+4x．设f（x）在[2n﹣2，2n）上的最大值为an（n∈N*），且{an}的前n项和为Sn ， 则Sn=（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在同一平面内，点P位于两平行直线l1、l2两侧，且P到l1 ， l2的距离分别为1，3，点M，N分别在l1 ， l2上，|
+ 
|=8，则 的最大值为（ ） 
A.15
B.12
C.10
D.9 -
科目： 来源： 题型：
查看答案和解析>>【题目】如下图所示，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE＝3AF，BE与平面ABCD所成的角为60°.
(1)求证：AC⊥平面BDE；
(2)求二面角F－BE－D的余弦值；
(3)设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．
相关试题
