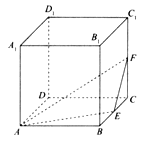
【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
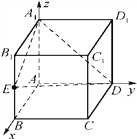
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
参考答案:
【答案】 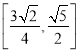
![]()
【解析】(文科选做)如下图所示:
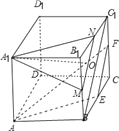
取棱BB1、B1C1的中点M、N,连接MN,连接BC1,
∵M、N、E、F为所在棱的中点,
∴MN∥BC1,EF∥BC1,
∴MN∥EF,
又MN平面AEF,EF平面AEF,
∴MN∥平面AEF;
∵AA1∥NE,AA1=NE,
∴四边形AENA1为平行四边形,
∴A1N∥AE,又A1N平面AEF,AE平面AEF,
∴A1N∥平面AEF,
又A1N∩MN=N,
∴平面A1MN∥平面AEF,
∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
∴点P必在线段MN上。
在Rt△A1B1M中, 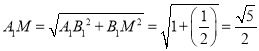 ,
,
同理在Rt△A1B1N中,可求得![]() ,
,
∴△A1MN为等腰三角形,
当P在MN中点O时A1P⊥MN,此时A1P最短,P位于M或N处时A1P最长,
又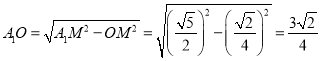 .
.
所以线段A1P长度的取值范围是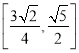 .答案:
.答案: 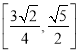 。
。
-
科目: 来源: 题型:
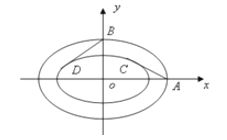
查看答案和解析>>【题目】某奥运会主体育场的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,我们称这两个椭圆相似。
(1)已知椭圆
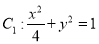 ,写出与椭圆
,写出与椭圆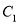 相似且焦点在
相似且焦点在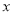 轴上、短半轴长为
轴上、短半轴长为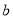 的椭圆
的椭圆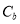 的标准方程;若在椭圆
的标准方程;若在椭圆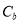 上存在两点
上存在两点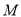 、
、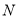 关于直线
关于直线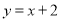 对称,求实数
对称,求实数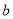 的取值范围;
的取值范围;(2)从外层椭圆顶点A、B向内层椭圆引切线AC、BD,设内层椭圆方程为
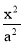 +
+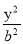 =1 (a
=1 (a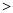 b
b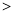 0),AC与BD的斜率之积为-
0),AC与BD的斜率之积为-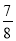 ,求椭圆的离心率。
,求椭圆的离心率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,命题
,命题 椭圆C1:
椭圆C1:  表示的是焦点在
表示的是焦点在 轴上的椭圆,命题
轴上的椭圆,命题 对
对 ,直线
,直线 与椭圆C2:
与椭圆C2:  恒有公共点.
恒有公共点.(1)若命题“
 ”是假命题,命题“
”是假命题,命题“ ”是真命题,求实数
”是真命题,求实数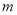 的取值范围.
的取值范围.(2)若
 真
真 假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
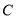 :
: 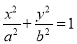 (
(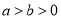 )与
)与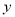 轴交于
轴交于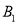 ,
, 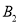 两点,
两点, 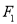 为椭圆
为椭圆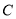 的左焦点,且
的左焦点,且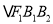 是边长为2的等边三角形.
是边长为2的等边三角形.(Ⅰ)求椭圆
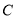 的方程;
的方程;(Ⅱ)设直线
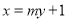 与椭圆
与椭圆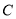 交于
交于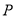 ,
, 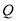 两点,点
两点,点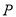 关于
关于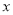 轴的对称点为
轴的对称点为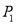 (
(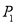 与
与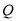 不重合),则直线
不重合),则直线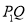 与
与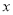 轴交于点
轴交于点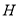 ,求
,求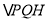 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
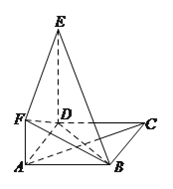
查看答案和解析>>【题目】如图所示,正方形
 与直角梯形
与直角梯形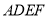 所在平面互相垂直,
所在平面互相垂直, 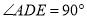 ,
, 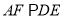 ,
, 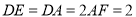 .
.
(I)求证:
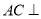 平面
平面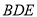 .
.(II)求证:
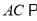 平面
平面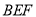 .
.(III)求四面体
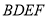 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某钢厂打算租用
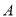 ,
, 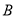 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材, 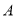 ,
, 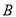 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且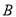 型车皮不多于
型车皮不多于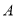 型车皮7个,分别用
型车皮7个,分别用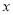 ,
, 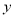 表示租用
表示租用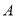 ,
,  两种车皮的个数.
两种车皮的个数.(Ⅰ)用
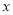 ,
, 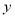 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;(Ⅱ)分别租用
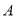 ,
, 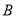 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱
 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是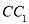 棱的中点,AE交
棱的中点,AE交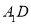 于点H.
于点H.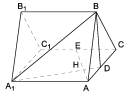
(1)求证:
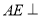 平面
平面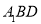 ;
;(2)求二面角
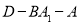 的余弦值;
的余弦值;(3)求点
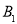 到平面
到平面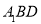 的距离.
的距离.
相关试题

