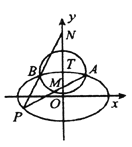
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1)依据题设条件求出参数即可;(2)依据题设条件及向量的数量积公式建立目标函数,再借助该函数取得最小值时求出圆的方程;(3)借助直线与椭圆的位置关系进行分析推证:
试题解析:
(1) 由题意知, ![]() ,得
,得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(2) ![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,设
轴对称,设![]() ,由点
,由点![]() 椭圆
椭圆![]() 上,则
上,则![]() ,得
,得![]()
![]() .由题意知,
.由题意知, ![]() ,
,![]() 当
当![]() 时,
时, ![]() 取得最小值
取得最小值![]() .此时,
.此时, ![]() ,故
,故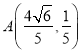 .又点
.又点![]() 在圆
在圆![]() 上,代入圆的方程,得
上,代入圆的方程,得![]() .
.
故圆![]() 的方程为
的方程为![]() .
.
(3)设![]() ,则
,则![]() 的方程为
的方程为![]() .令
.令![]() ,得
,得![]() .同理可得,
.同理可得, ![]() . 故
. 故![]() . ①
. ①
![]() 都在椭圆
都在椭圆![]() 上,
上, ![]() ,代入①得,
,代入①得, 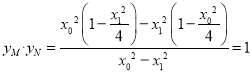 .即得
.即得![]() 为定值.
为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北
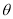 的方向移动,距台风中心
的方向移动,距台风中心 千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则
千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则 和
和 的值分别为(附:
的值分别为(附: 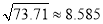 )( )
)( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的对角线
的对角线 与
与 相交于点
相交于点 ,四边形
,四边形 为矩形,平面
为矩形,平面 平面
平面 .
.
(1)求证:平面
 平面
平面 ;
;(2)若点
 在线段
在线段 上,且
上,且 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设偶函数f(x)满足f(x)=x3﹣8(x≥0),则{x|f(x﹣2)>0}=( )
A.{x|x<﹣2或x>4}
B.{x|x<0或x>4}
C.{x|x<0或x>6}
D.{x|x<﹣2或x>2} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
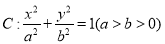 ,离心率
,离心率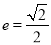 ,它的长轴长等于圆
,它的长轴长等于圆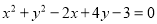 的直径.
的直径.(1)求椭圆
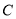 的方程;
的方程;(2)若过点
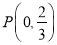 的直线
的直线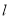 交椭圆
交椭圆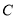 于
于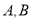 两点,是否存在定点
两点,是否存在定点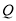 ,使得以
,使得以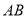 为直径的圆经过这个定点,若存在,求出定点
为直径的圆经过这个定点,若存在,求出定点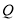 的坐标;若不存在,请说明理由?
的坐标;若不存在,请说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
 中,
中,  平面
平面 ,
,  平面
平面 ,
,  ,
,  ,又
,又 ,
,  .
.
(1)求
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
相关试题

