【题目】设偶函数f(x)满足f(x)=x3﹣8(x≥0),则{x|f(x﹣2)>0}=( )
A.{x|x<﹣2或x>4}
B.{x|x<0或x>4}
C.{x|x<0或x>6}
D.{x|x<﹣2或x>2}
参考答案:
【答案】B
【解析】解:当x<0时,则﹣x>0,由偶函数f(x)满足f(x)=x3﹣8(x≥0)
可得,f(x)=f(﹣x)=﹣x3﹣8,
则 f(x)= ![]() ,
,
∴f(x﹣2)= ![]()
令f(x﹣2)>0,
当x﹣2≥0,即x≥2时,有(x﹣2)3﹣8>0可解得x>4,
当x﹣2<0,即x<2时,有﹣(x﹣2)3﹣8>0,可解得x<0.
即x>4或x<0.
故选B.
【考点精析】认真审题,首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的对角线
的对角线 与
与 相交于点
相交于点 ,四边形
,四边形 为矩形,平面
为矩形,平面 平面
平面 .
.
(1)求证:平面
 平面
平面 ;
;(2)若点
 在线段
在线段 上,且
上,且 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
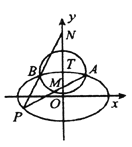
查看答案和解析>>【题目】如图,椭圆
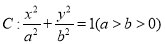 的离心率为
的离心率为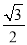 ,以椭圆
,以椭圆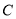 的上顶点
的上顶点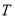 为圆心作圆,
为圆心作圆,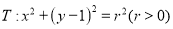 ,圆
,圆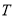 与椭圆
与椭圆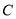 在第一象限交于点
在第一象限交于点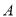 ,在第二象限交于点
,在第二象限交于点 .
.
(1)求椭圆
 的方程;
的方程;(2)求
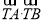 的最小值,并求出此时圆
的最小值,并求出此时圆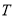 的方程;
的方程;(3)设点
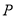 是椭圆
是椭圆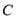 上异于
上异于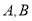 的一点,且直线
的一点,且直线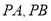 分别与
分别与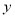 轴交于点
轴交于点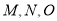 为坐标原点,求证:
为坐标原点,求证: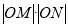 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
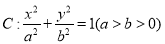 ,离心率
,离心率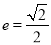 ,它的长轴长等于圆
,它的长轴长等于圆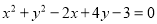 的直径.
的直径.(1)求椭圆
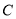 的方程;
的方程;(2)若过点
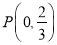 的直线
的直线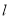 交椭圆
交椭圆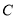 于
于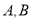 两点,是否存在定点
两点,是否存在定点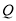 ,使得以
,使得以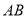 为直径的圆经过这个定点,若存在,求出定点
为直径的圆经过这个定点,若存在,求出定点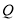 的坐标;若不存在,请说明理由?
的坐标;若不存在,请说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
 中,
中,  平面
平面 ,
,  平面
平面 ,
,  ,
,  ,又
,又 ,
,  .
.
(1)求
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为
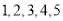 的五批疫苗,供全市所辖的
的五批疫苗,供全市所辖的 三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种. (1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记
 三个区选择的疫苗批号的中位数为
三个区选择的疫苗批号的中位数为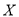 ,求
,求  的分布列及期望.
的分布列及期望.
相关试题

