【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
参考答案:
【答案】B
【解析】设塔的顶层共有灯![]() 盏,则各层的灯数构成一个首项为
盏,则各层的灯数构成一个首项为![]() ,公比为2的等比数列,结合等比数列的求和公式有:
,公比为2的等比数列,结合等比数列的求和公式有: ![]() ,解得
,解得![]() ,即塔的顶层共有灯3盏,故选B.
,即塔的顶层共有灯3盏,故选B.
点睛:用数列知识解相关的实际问题,关键是列出相关信息,合理建立数学模型——数列模型,判断是等差数列还是等比数列模型;求解时要明确目标,即搞清是求和、求通项、还是解递推关系问题,所求结论对应的是解方程问题、解不等式问题、还是最值问题,然后将经过数学推理与计算得出的结果放回到实际问题中,进行检验,最终得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,角A,B,C的对边分别是a,b,c,且2cos2
 =
= 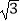 sinB,a=3c.
sinB,a=3c.
(1)求角B的大小和tanC的值;
(2)若b=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
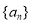 的前
的前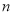 项和为
项和为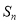 ,
, 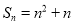 ,数列
,数列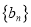 的通项公式为
的通项公式为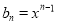 .
.(1)求数列
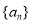 的通项公式;
的通项公式;(2)设
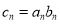 ,数列
,数列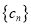 的前
的前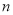 项和为
项和为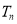 ,
,①求
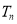 ;
;②若
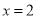 ,求数列
,求数列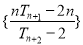 的最小项的值.
的最小项的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是公差为2的等差数列,且a1 , a4 , a13成等比数列,数列{
 }是首项为1,公比为3的等比数列.
}是首项为1,公比为3的等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设数列{an+bn}的前n项和Rn , 若不等式 ≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
≤λ3n+n+3对n∈N*恒成立,求λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取
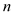 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:组数
分组
低碳族的人数
占本组的频率
第一组
[25,30)
120
0.6
第二组
[30,35)
195
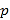
第三组
[35,40)
100
0.5
第四组
[40,45)

0.4
第五组
[45,50)
30
0.3
第六组
[50,55]
15
0.3
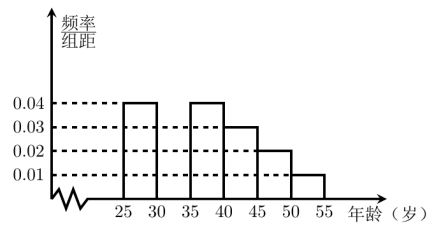
(1)补全频率分布直方图并求
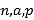 的值;
的值;(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在菱形
 中,
中,  ,
,  为
为 的中点,现将四边形
的中点,现将四边形 沿
沿 折起至
折起至 ,如图2.
,如图2.
(1)求证:
 面
面 ;
;(2)若二面角
 的大小为
的大小为 ,求平面
,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
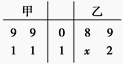
查看答案和解析>>【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
相关试题

