【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() (2) 减函数,证明见解析;(3)
(2) 减函数,证明见解析;(3) ![]() .
.
【解析】
(1)利用奇函数的性质令![]() ,求解
,求解![]() 即可.
即可.
(2)利用函数的单调性的定义证明即可.
(3)利用函数是奇函数以及函数的单调性转化不等式为代数形式的不等式,求解即可.
(1)∵![]() 在定义域
在定义域![]() 上是奇函数,
上是奇函数,
所以![]() ,即
,即![]() ,∴
,∴![]() ,
,
经检验,当![]() 时,原函数是奇函数.
时,原函数是奇函数.
(2)![]() 在
在![]() 上是减函数,证明如下:
上是减函数,证明如下:
由(1)知![]() ,
,
任取![]() ,设
,设![]() ,
,
则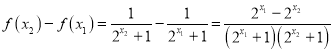 ,
,
∵函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() ,
,
∴函数![]() 在
在![]() 上是减函数.
上是减函数.
(3)因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于![]() ,
,
由(2)知![]() 在
在![]() 上是减函数,由上式推得
上是减函数,由上式推得![]() ,
,
即对任意![]() ,有
,有![]() 恒成立,
恒成立,
由 ,
,
令![]() ,
,![]() ,则可设
,则可设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
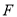 为椭圆
为椭圆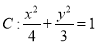 的右焦点,
的右焦点, 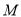 为
为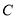 上的任意一点.
上的任意一点. (1)求
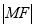 的取值范围;
的取值范围;(2)
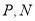 是
是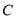 上异于
上异于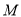 的两点,若直线
的两点,若直线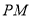 与直线
与直线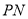 的斜率之积为
的斜率之积为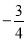 ,证明:
,证明: 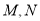 两点的横坐标之和为常数.
两点的横坐标之和为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
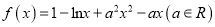 .
.(1)讨论函数
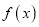 的单调性;
的单调性;(2)若
 且
且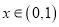 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018届福建省福州市高三上学期期末】过椭圆
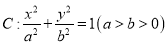 的右焦点作
的右焦点作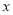 轴的垂线,交
轴的垂线,交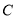 于
于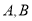 两点,直线
两点,直线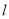 过
过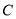 的左焦点和上顶点.若以
的左焦点和上顶点.若以 为直径的圆与
为直径的圆与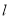 存在公共点,则
存在公共点,则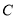 的离心率的取值范围是( )
的离心率的取值范围是( )A.
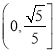 B.
B. 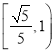 C.
C. 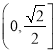 D.
D. 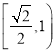
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
0.16
70.5~80.5
10
80.5~90.5
16
0.32
90.5~100.5
合计
50
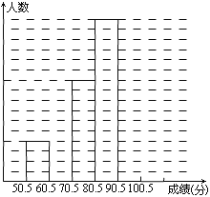
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为其上一点,且有
为其上一点,且有
(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)过
 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,过
两点,过 与
与 平行的直线
平行的直线 与椭圆
与椭圆 交于
交于 两点,求四边形
两点,求四边形 的面积
的面积 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
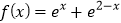 ,若关于
,若关于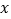 的不等式
的不等式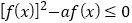 恰有3个整数解,则实数
恰有3个整数解,则实数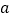 的最小值为( )
的最小值为( )A. 1 B.
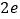 C.
C. 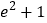 D.
D. 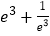
相关试题

