【题目】已知![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性,并予以证明。
的奇偶性,并予以证明。
参考答案:
【答案】(1)(-1,1)(2)奇函数
【解析】
(1)由题意可得f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,由
,由 ![]() 求得函数的定义域;
求得函数的定义域;
(2)由于f(x)﹣g(x)=![]() ,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),可得h(﹣x)=﹣h(x),从而得到函数h(x)=f(x)﹣g(x)为奇函数.
,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),可得h(﹣x)=﹣h(x),从而得到函数h(x)=f(x)﹣g(x)为奇函数.
(1)由于f(x)=loga(1+x),g(x)=loga(1﹣x),故f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,
,
由 ![]() ,求得﹣1<x<1,故函数的定义域为(﹣1,1).
,求得﹣1<x<1,故函数的定义域为(﹣1,1).
(2)由于f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),
,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),
可得h(﹣x)=![]() =﹣
=﹣![]() =﹣h(x),故函数h(x)=f(x)﹣g(x)为奇函数.
=﹣h(x),故函数h(x)=f(x)﹣g(x)为奇函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线y2=8x的焦点为F,过点F作直线l与抛物线分别交于A,B两点,若点M满足
 =
=  (
( 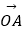 +
+  ),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家发现视觉和空间能力与性别有关,孝感市黄陂路高中数学兴趣小组为了验证这个结论,从兴趣小组中抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)能否据此判断有
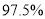 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?(2)以上列联表中女生选做几何题的频率作为概率,从该校1500名女生中随机选6名女生,记6名女生选做几何题的人数为
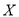 ,求
,求 的数学期望
的数学期望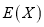 和方差
和方差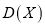 .
.附表:

参考公式:
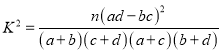 ,其中
,其中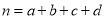 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,a,b,c为角A,B,C所对的边,且2cos2
 +(cosB﹣
+(cosB﹣  sinB)cosA=1.
sinB)cosA=1.
(1)求角A的值;
(2)求f(x)=4cosxcos(x﹣A)在x∈[0, ]的值域.
]的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形
 中,
中, 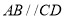 ,
, 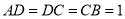 ,
, 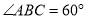 ,四边形
,四边形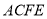 为矩形,平面
为矩形,平面 平面
平面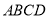 ,
, 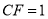 .
.
(1)求证:
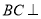 平面
平面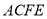 ;
;(2)点
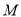 在线段
在线段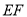 上运动,设平面
上运动,设平面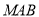 与平面
与平面 所成二面角的平面角为
所成二面角的平面角为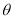 ,试求
,试求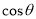 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
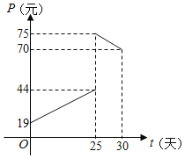
(1)请确定销售价格P(元)和时间t(天)的函数解析式;
(2)该商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)求该商品的日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 (
( )的离心率是
)的离心率是 ,点
,点 在短轴
在短轴 上,且
上,且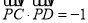 。
。(1)球椭圆
 的方程;
的方程;(2)设
 为坐标原点,过点
为坐标原点,过点 的动直线与椭圆交于
的动直线与椭圆交于 两点。是否存在常数
两点。是否存在常数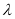 ,使得
,使得 为定值?若存在,求
为定值?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
相关试题

