【题目】已知点![]() ,圆
,圆![]() .
.
(![]() )设
)设![]() ,求过点
,求过点![]() 且与圆
且与圆![]() 相切的直线方程.
相切的直线方程.
(![]() )设
)设![]() ,直线
,直线![]() 过点
过点![]() 且被圆
且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
(![]() )设
)设![]() ,直线
,直线![]() 过点
过点![]() ,求
,求![]() 被圆
被圆![]() 截得的线段的最短长度,并求此时
截得的线段的最短长度,并求此时![]() 的方程.
的方程.
参考答案:
【答案】(1)切线方程为![]() 或
或![]() ;(2)直线
;(2)直线![]() 的方程为
的方程为![]() 或
或![]() ;(3)
;(3)![]() 方程为即
方程为即![]() .
.
【解析】试题分析:(1)已知直线上一点,设出直线方程,点斜式,再根据直线和圆的位置关系,![]() ,解得
,解得![]() ,求得方程。(2)根据垂径定理
,求得方程。(2)根据垂径定理![]() ,即圆心到直线
,即圆心到直线![]() 的距离为
的距离为![]() ,得到结果。(3)首先要分析出来线段最短时直线和圆的位置关系:
,得到结果。(3)首先要分析出来线段最短时直线和圆的位置关系:![]() ,故当
,故当![]() 时,
时,![]() ,再根据垂径定理得到直线的斜率。
,再根据垂径定理得到直线的斜率。
(![]() )解:如图所示,此时
)解:如图所示,此时![]() ,
,
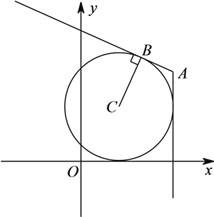
设切线为![]() 或
或![]() ,
,
验证知![]() 与题意相符;
与题意相符;
当切线为![]() ,即
,即![]() 时,
时,
圆心![]() 到切线的距离
到切线的距离
![]() ,解得
,解得![]() ,
,
所以,切线方程为![]() 或
或![]() .
.
(![]() )如图所示,此时
)如图所示,此时![]() ,
,
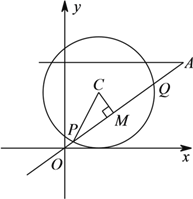
设直线![]() 为
为![]() 或
或![]() (舍),
(舍),
设弦![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,即圆心到直线
,即圆心到直线![]() 的距离为
的距离为![]() ,
,
于是![]() ,解得
,解得![]() 或
或![]() ,
,
所以,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(![]() )如图所示,此时
)如图所示,此时![]() ,
,

设所截得的线段为![]() ,圆心到直线
,圆心到直线![]() 的距离为
的距离为![]() ,则
,则
![]() ,
,
即![]() ,因为直线
,因为直线![]() 过点
过点![]() ,
,
所以圆心到直线![]() 的距离为
的距离为
![]() ,故当
,故当![]() 时,
时,![]() ,
,
此时![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
故直线![]() 方程为
方程为![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
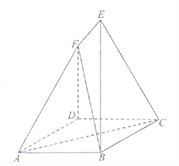
查看答案和解析>>【题目】如图,
 是边长为
是边长为 的菱形,
的菱形,  ,
,  平面
平面 ,
,  平面
平面 ,
,  .
.
(Ⅰ)求证:
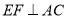 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组
频数
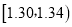
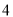
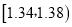
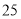
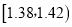
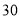
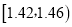
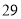
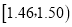
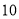
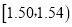
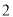
合计
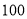
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在
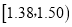 中的概率及纤度小于
中的概率及纤度小于 的概率是多少?
的概率是多少?(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是 ( )
A. 如果平面
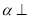 平面
平面 ,那么平面
,那么平面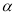 内一定存在直线平行于平面
内一定存在直线平行于平面
B. 如果平面
 不垂直平面
不垂直平面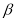 ,那么平面
,那么平面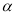 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面
C. 如果平面
 平面
平面 ,平面
,平面 平面
平面 ,且
,且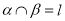 ,那么
,那么
D. 如果平面
 平面
平面 ,那么平面
,那么平面 内所有直线都垂直于平面
内所有直线都垂直于平面
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
(Ⅰ)已知
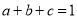 ,证明:
,证明:  ;
;(Ⅱ)若对任意实数
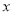 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=

-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱
 ,侧棱与底面垂直,
,侧棱与底面垂直, ,
, ,
, ,
, 分别是
分别是 ,
,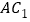 的中点.
的中点.
(
 )求证:
)求证: 平面
平面 .
.(
 )求证:平面
)求证:平面 平面
平面 .
.
相关试题

