【题目】设fn(x)=(3n﹣1)x2﹣x(n∈N*),An={x|fn(x)<0}
(1)定义An={x|x1<x<x2}的长度为x2﹣x1 , 求An的长度;
(2)把An的长度记作数列{an},令bn=anan+1;
1°求数列{bn}的前n项和Sn;
2°是否存在正整数m,n(1<m<n),使得S1 , Sm , Sn成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由fn(x)<0得(3n﹣1)x2﹣x<0,∴0<x< ![]() ,
,
∴An的长度为 ![]()
(2)解:1°、an= ![]() ,bn=anan+1=
,bn=anan+1= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴数列{bn}的前n项和Sn= ![]() [(
[( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )]=
)]= ![]() ;
;
2°、由1°可知S1= ![]() ,Sm=
,Sm= ![]() ,Sn=
,Sn= ![]() ,
,
假设存在正整数m,n(1<m<n),使得S1,Sm,Sn成等比数列,
则Sm2=S1Sn,化简得(﹣3m2+6m+2)n=5m2,
m=2时,n=10;
m≥3时,﹣3m2+6m+2<0,5m2>0,等式不成立,
综上所述,存在正整数m=2,n=10,使得S1,Sm,Sn成等比数列
【解析】(1)利用新定义,即可求An的长度;(2)1°利用裂项法可求得Sn;
2°假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,可求得(﹣3m2+6m+2)n=5m2 , 由1<m<n,验证可求得结论.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线
 上有一点
上有一点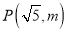 (
( ),点
),点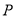 在
在 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线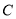 的右焦点,过点
的右焦点,过点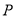 作双曲线
作双曲线 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为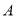 ,
, 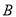 ,若平行四边形
,若平行四边形 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )A.
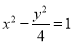 B.
B. 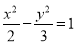 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为
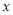 元时,销售量可达到
元时,销售量可达到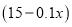 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价 供货价格.问:
供货价格.问:(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
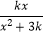 (k>0).
(k>0).
(1)若f(x)>m的解集为{x|x<﹣3或x>﹣2},求不等式5mx2+ x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
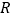 上的函数
上的函数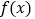 为增函数,对任意
为增函数,对任意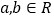 都有
都有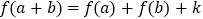 (
(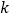 为常数)
为常数)(1)判断
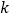 为何值时,
为何值时,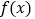 为奇函数,并证明;
为奇函数,并证明;(2)设
 ,
,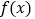 是
是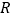 上的增函数,且
上的增函数,且 ,若不等式
,若不等式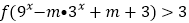 对任意
对任意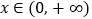 恒成立,求实数
恒成立,求实数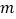 的取值范围.
的取值范围.(3)若
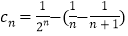 ,
,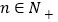 ,
,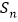 为
为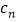 的前
的前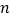 项和,求正整数
项和,求正整数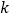 ,使得对任意
,使得对任意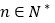 均有
均有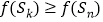 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
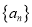 是正数组成的数列,
是正数组成的数列, 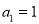 ,且点
,且点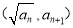
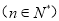 在函数
在函数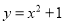 的图象上.
的图象上.(1)求数列
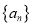 的通项公式;
的通项公式;(2)若列数
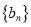 满足
满足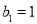 ,
,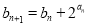 ,求证:
,求证: 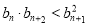
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
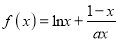 ,(
,( 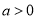 )
)(1)当
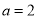 时,求函数
时,求函数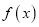 在
在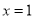 处的切线方程;
处的切线方程;(2)若函数
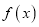 在区间
在区间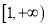 上单调递增,求
上单调递增,求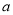 的取值范围;
的取值范围;(3)求函数
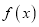 在区间
在区间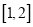 的最小值.
的最小值.
相关试题

