【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)存在点
;(Ⅱ)存在点![]() 或
或![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列.
的斜率始终成等差数列.
【解析】
试题分析:(Ⅰ)因为直线过焦点,所以设直线![]() ,与抛物线方程联立,转化为
,与抛物线方程联立,转化为![]() ,利用焦点弦长公式
,利用焦点弦长公式![]() ,
,![]() ,解得直线方程;
,解得直线方程;
(Ⅱ)设![]() ,用坐标表示直线
,用坐标表示直线![]() 的斜率,若成等差数列,那么
的斜率,若成等差数列,那么![]() ,代入(1)的坐标后,若恒成立,解得点
,代入(1)的坐标后,若恒成立,解得点![]() 的坐标.
的坐标.
试题解析:(Ⅰ)焦点![]() ∵直线
∵直线![]() 的斜率不为
的斜率不为![]() ,所以设
,所以设![]() ,
,
![]() ,
,![]() 由
由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() , ∴
, ∴![]() . ∴直线
. ∴直线![]() 的斜率
的斜率![]() ,
,
∵![]() ,∴
,∴![]() , ∴直线
, ∴直线![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,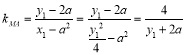 ,
,
同理![]() ,
,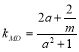 ,
,
∵直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,
的斜率始终成等差数列,
∴![]() 恒成立,
恒成立,
即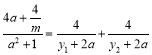 恒成立.
恒成立.
∴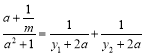
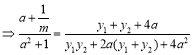 ,
,
把![]() ,
,![]() 代入上式,得
代入上式,得![]() 恒成立,
恒成立,![]() .
.
∴存在点![]() 或
或![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列.
的斜率始终成等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢
不喜欢
合计
大于40岁
20
5
25
20岁至40岁
10
20
30
合计
30
25
55
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
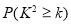
0.15
0.10
0.05
0.025
0.010
0.005
0.001
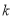
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
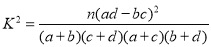 ,其中
,其中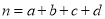 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
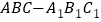 中,
中,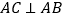 ,
,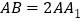 ,
,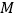 是
是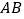 的中点,
的中点,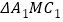 是等腰三角形,
是等腰三角形,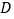 为
为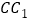 的中点,
的中点,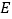 为
为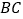 上一点.
上一点.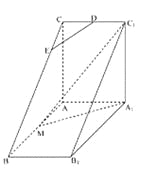
(I)若
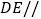 平面
平面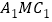 ,求
,求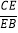 ;
;(II)平面
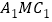 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,向量
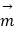 =(a+b,sinA﹣sinC),且
=(a+b,sinA﹣sinC),且 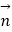 =(c,sinA﹣sinB),且
=(c,sinA﹣sinB),且 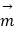 ∥
∥ 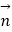 .
.
(1)求角B的大小;
(2)若a+c=8,求AC边上中线长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线
 上有一点
上有一点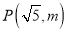 (
( ),点
),点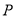 在
在 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线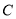 的右焦点,过点
的右焦点,过点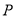 作双曲线
作双曲线 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为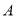 ,
, 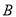 ,若平行四边形
,若平行四边形 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )A.
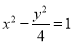 B.
B. 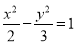 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为
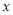 元时,销售量可达到
元时,销售量可达到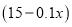 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价 供货价格.问:
供货价格.问:(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
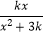 (k>0).
(k>0).
(1)若f(x)>m的解集为{x|x<﹣3或x>﹣2},求不等式5mx2+ x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范围.
相关试题

