【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 、
、![]() 在棱
在棱![]() 上,动点
上,动点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 大于零),则四面体
大于零),则四面体![]() 的体积( ).
的体积( ).
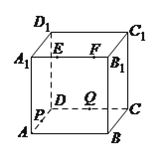
A. 与![]() ,
,![]() ,
,![]() 都有关 B. 与
都有关 B. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
C. 与![]() 有关,与
有关,与![]() ,
,![]() 无关 D. 与
无关 D. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
参考答案:
【答案】D
【解析】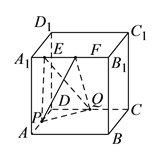
如图:![]() 在棱
在棱![]() 上,
上,![]() 在棱
在棱![]() 上,
上,![]() ,所以
,所以![]() 的高为定值,又
的高为定值,又![]() 为定值
为定值![]() ,所以
,所以![]() 的面积为定值,四面体
的面积为定值,四面体![]() 的体积与点
的体积与点![]() 到平面
到平面![]() 的距离有关,即与
的距离有关,即与![]() 的大小有关,故选
的大小有关,故选![]() .
.
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.
(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
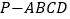 中,
中,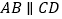 ,
,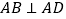 ,
,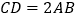 ,平面
,平面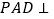 平面
平面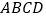 ,
,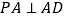 .
.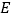 和
和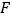 分别是
分别是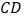 和
和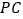 的中点.
的中点.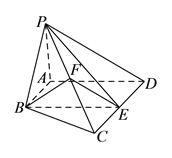
求证:(I)
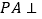 底面
底面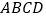 .
.(II)平面
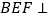 平面
平面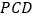 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱柱
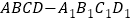 中,
中,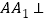 底面
底面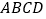 ,底面
,底面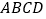 为菱形,
为菱形,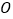 为
为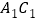 与
与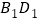 交点,已知
交点,已知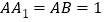 ,
,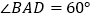 .
.(I)求证:
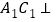 平面
平面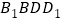 .
.(II)在线段
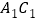 上是否存在一点
上是否存在一点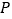 ,使得
,使得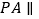 平面
平面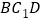 ,如果存在,求
,如果存在,求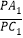 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.(III)设点
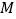 在
在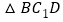 内(含边界),且
内(含边界),且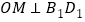 ,求所有满足条件的点
,求所有满足条件的点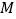 构成的图形,并求
构成的图形,并求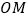 的最小值.
的最小值.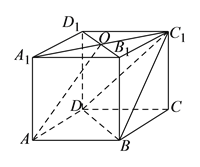
-
科目: 来源: 题型:
查看答案和解析>>【题目】若存在实数
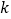 和
和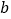 ,使得函数
,使得函数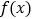 和
和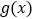 对定义域内的任意
对定义域内的任意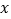 均满足:
均满足: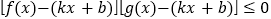 ,且存在
,且存在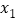 使得
使得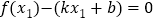 ,存在
,存在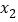 使得
使得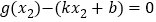 ,则称直线
,则称直线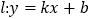 为函数
为函数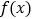 和
和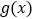 的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).
的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).①任意两个一次函数最多存在一条“分界线”;
②“分界线”存在的两个函数的图象最多只有两个交点;
③
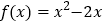 与
与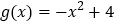 的“分界线”是
的“分界线”是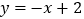 ;
;④
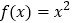 与
与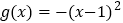 的“分界线”是
的“分界线”是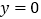 或
或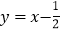 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
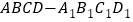 中,
中,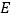 、
、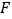 为棱
为棱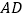 、
、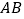 的中点.
的中点.(Ⅰ)求证:
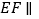 平面
平面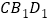 .
.(Ⅱ)求证:平面
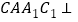 平面
平面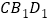 .
.(Ⅲ)若正方体棱长为
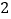 ,求三棱锥
,求三棱锥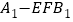 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ )的一个对称中心是(
)的一个对称中心是(  ,0);
,0);
④函数y=sin(x+ )在闭区间[﹣
)在闭区间[﹣  ,
,  ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: . -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:关于x的不等式
 的解集为
的解集为 ;命题q:函数
;命题q:函数 为增函数.命题r:a满足
为增函数.命题r:a满足 .
.(1)若p∨q是真命题且p∧q是假题.求实数a的取值范围.
(2)试判断命题¬p是命题r成立的一个什么条件.
相关试题

