【题目】在四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.
(I)求证:![]() 平面
平面![]() .
.
(II)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,如果存在,求
,如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
(III)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]() ,求所有满足条件的点
,求所有满足条件的点![]() 构成的图形,并求
构成的图形,并求![]() 的最小值.
的最小值.
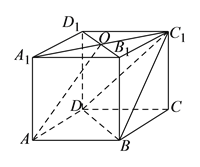
参考答案:
【答案】(1)见解析(2)![]() (3)构成的图形是线段
(3)构成的图形是线段![]() ,包括端点,
,包括端点,![]()
【解析】试题分析:(1)由线面垂直得![]() ,由菱形性质得
,由菱形性质得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() ,(2)连接
,(2)连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 是
是![]() 中点,由平几知识可得
中点,由平几知识可得![]() 是平行四边形,即得
是平行四边形,即得![]() ,再由线面平行判定定理得结论(3)由线面垂直性质与判定定理可得
,再由线面平行判定定理得结论(3)由线面垂直性质与判定定理可得![]() ,即得点
,即得点![]() 构成的图形是线段
构成的图形是线段![]() ,再利用三角形面积求O到直线
,再利用三角形面积求O到直线![]() 距离,即得
距离,即得![]() 的最小值.
的最小值.
试题解析:(I)证明:∵![]() 底面
底面![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为菱形,
为菱形,
∴![]() ,
,
而![]() ,
,
∴![]() 平面
平面![]() .
.
(II)存在点![]() ,当
,当![]() 是
是![]() 中点,即
中点,即![]() 时,
时,![]() 平面
平面![]() .
.

证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 中点,
中点,
∵![]() ,且
,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴当点![]() 与点
与点![]() 重合时,
重合时,![]() 平面
平面![]() ,
,
此时,![]() .
.
(III)在![]() 内,满足
内,满足![]() 的点构成的图形是线段
的点构成的图形是线段![]() ,包括端点,
,包括端点,
连接![]() ,则
,则![]() ,
,
∵![]() ,
,
∴要使![]() ,只需
,只需![]() ,从而需
,从而需![]() ,
,
又在![]() 中,
中,![]() ,
,
又![]() 为
为![]() 中点,
中点,
∴![]() ,
,
故![]() 点一定在线段
点一定在线段![]() 上,
上,
当![]() 时,
时,![]() 取最小值.
取最小值.
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
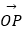 =(2,1),
=(2,1), 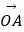 =(1,7),
=(1,7), 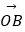 =(5,1),设X是直线OP上的一点(O为坐标原点),那么
=(5,1),设X是直线OP上的一点(O为坐标原点),那么 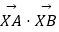 的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程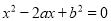 .
.(1)若
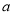 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 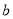 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
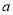 时从区间
时从区间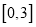 上任取的一个数,
上任取的一个数, 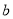 是从区间
是从区间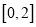 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
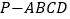 中,
中,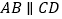 ,
,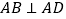 ,
,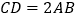 ,平面
,平面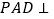 平面
平面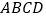 ,
,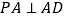 .
.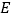 和
和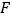 分别是
分别是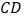 和
和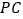 的中点.
的中点.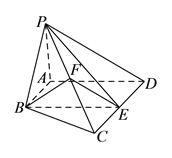
求证:(I)
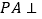 底面
底面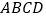 .
.(II)平面
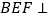 平面
平面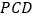 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若存在实数
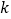 和
和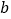 ,使得函数
,使得函数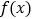 和
和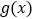 对定义域内的任意
对定义域内的任意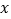 均满足:
均满足: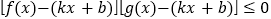 ,且存在
,且存在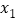 使得
使得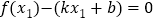 ,存在
,存在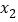 使得
使得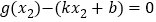 ,则称直线
,则称直线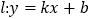 为函数
为函数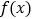 和
和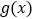 的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).
的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).①任意两个一次函数最多存在一条“分界线”;
②“分界线”存在的两个函数的图象最多只有两个交点;
③
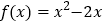 与
与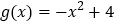 的“分界线”是
的“分界线”是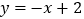 ;
;④
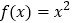 与
与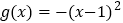 的“分界线”是
的“分界线”是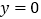 或
或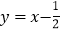 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
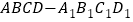 的棱长为
的棱长为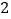 ,动点
,动点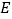 、
、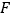 在棱
在棱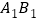 上,动点
上,动点 ,
, 分别在棱
分别在棱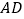 ,
, 上,若
上,若 ,
, ,
,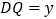 ,
, (
( ,
,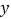 ,
,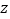 大于零),则四面体
大于零),则四面体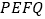 的体积( ).
的体积( ).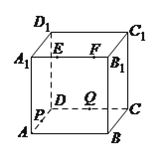
A. 与
 ,
,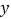 ,
,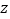 都有关 B. 与
都有关 B. 与 有关,与
有关,与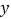 ,
,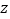 无关
无关C. 与
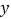 有关,与
有关,与 ,
,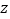 无关 D. 与
无关 D. 与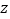 有关,与
有关,与 ,
,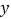 无关
无关 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
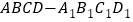 中,
中,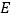 、
、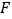 为棱
为棱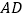 、
、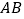 的中点.
的中点.(Ⅰ)求证:
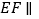 平面
平面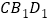 .
.(Ⅱ)求证:平面
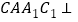 平面
平面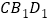 .
.(Ⅲ)若正方体棱长为
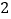 ,求三棱锥
,求三棱锥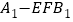 的体积.
的体积.
相关试题

