【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.数据表明,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组比第七组少1人. 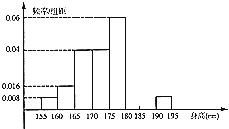
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x,y,求满足“|x﹣y|≤5”的事件的概率.
参考答案:
【答案】
(1)解:由频率分布直方图得身高在180cm以上(含180cm)为最后三组,
则最后三组频率为(0.016+0.012+0.008)×5=0.18,
这所学校高三年级全体男生身高在180cm以上(含180cm)的人数为800×0.18=144
(2)解:由已知得身高在[180,185)内的人数为4,设为a、b、c、d,
身高在[190,195]内的人数为2,设为A、B,
若x,y∈[180,185)时,有ab、ac、ad、bc、bd、cd共6种情况;
若x,y∈[190,195]时,有AB共1种情况;
若x,y分别在[180,185)和[190,195]内时,有aA、bA、cA、dA、aB、bB、cB、dB,共8种情况.
所以,基本事件总数为6+1+8=15,
事件“|x﹣y|≤5”即取出两人在同一组,其所包含的基本事件个数有6+1=7,
所以P(|x﹣y|≤5)= ![]()
【解析】(1)由频率分布直方图得身高在180cm以上(含180cm)为最后三组,计算可得最后三组的频率,又由全校高三的总人数,计算可得高三年级全体男生身高在180cm以上人数;(2)根据题意,分析可得身高在[180,185)内的人数为4,设为a、b、c、d,身高在[190,195]内的人数为2,设为A、B,分类列举从6人中取出2人的情况,分析可得基本事件总数与事件“|x﹣y|≤5”所包含的基本事件数目,由古典概型公式,计算可得答案
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 ,左、右顶点分别为
,左、右顶点分别为 ,上、下顶点分别为
,上、下顶点分别为 ,四边形
,四边形 与四边形
与四边形 的面积之和为4.
的面积之和为4.(1)求椭圆
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 交于
交于 两点,
两点, (其中
(其中 为坐标原点),求直线
为坐标原点),求直线 被以线段
被以线段 为直径的圆截得的弦长.
为直径的圆截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
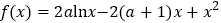
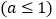 .
.(1)讨论
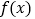 的单调性;
的单调性;(2)若
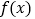 在区间
在区间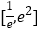 上有两个零点,求
上有两个零点,求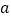 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
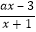 (a∈R).
(a∈R).
(1)若不等式f(x)<1的解集为(﹣1,4),求a的值;
(2)设a≤0,解关于x的不等式f(x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为( )

A.
B.
C.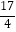
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠
 .
.
(1)求c;
(2)若C=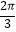 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
相关试题

