【题目】“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
参考答案:
【答案】B
【解析】解:∵数列{an}成等比数列,公比为q.∴an= ![]() .若a1<0时,则lgan+1没有意义.
.若a1<0时,则lgan+1没有意义.
由数列{lgan+1}成等差数列,则(lgan+1+1)﹣(lgan+1)= ![]() 为常数,则
为常数,则 ![]() 为非0常数.
为非0常数.
∴“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的必要不充分条件.
故选:B.
【考点精析】本题主要考查了等差关系的确定的相关知识点,需要掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列才能正确解答此题.
)那么这个数列就叫做等差数列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2+aln(x+1).
(1)求函数f(x)的单调区间;
(2)若函数F(x)=f(x)+ln 有两个极值点x1 , x2且x1<x2 , 求证F(x2)>
有两个极值点x1 , x2且x1<x2 , 求证F(x2)>  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为大力提倡“厉行节俭,反对浪费”,某高中通过随机询问100名性别不同的学生是否做到“光盘”行动,得到如表所示联表及附表:
做不到“光盘”行动
做到“光盘”行动
男
45
10
女
30
15
P(K2≥k0)
0.10
0.05
0.025
k0
2.706
3.841
5.024
经计算:K2=
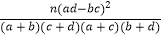 ≈3.03,参考附表,得到的正确结论是( )
≈3.03,参考附表,得到的正确结论是( )
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 ,左、右顶点分别为
,左、右顶点分别为 ,上、下顶点分别为
,上、下顶点分别为 ,四边形
,四边形 与四边形
与四边形 的面积之和为4.
的面积之和为4.(1)求椭圆
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 交于
交于 两点,
两点, (其中
(其中 为坐标原点),求直线
为坐标原点),求直线 被以线段
被以线段 为直径的圆截得的弦长.
为直径的圆截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
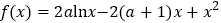
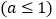 .
.(1)讨论
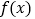 的单调性;
的单调性;(2)若
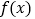 在区间
在区间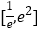 上有两个零点,求
上有两个零点,求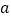 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.数据表明,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组比第七组少1人.
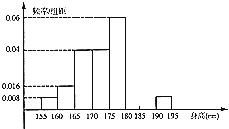
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x,y,求满足“|x﹣y|≤5”的事件的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
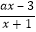 (a∈R).
(a∈R).
(1)若不等式f(x)<1的解集为(﹣1,4),求a的值;
(2)设a≤0,解关于x的不等式f(x)>0.
相关试题

