【题目】已知函数f(x)= ![]() ,a为常数且a>0.
,a为常数且a>0.
(1)f(x)的图象关于直线x= ![]() 对称;
对称;
(2)若x0满足f(f(x0))=x0 , 但f(x0)≠x0 , 则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1 , x2 , 试确定a的取值范围;
(3)对于(2)中的x1 , x2 , 和a,设x3为函数f(f(x))的最大值点,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),记△ABC的面积为S(a),讨论S(a)的单调性.
参考答案:
【答案】
(1)证明:∵ ![]() =
= ![]() =a(1﹣2|x|),
=a(1﹣2|x|), ![]() =a(1﹣2|x|),
=a(1﹣2|x|),
∴ ![]() ,∴f(x)的图象关于直线x=
,∴f(x)的图象关于直线x= ![]() 对称
对称
(2)解:当 ![]() 时,有f(f(x))=
时,有f(f(x))= 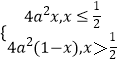 .
.
∴f(f(x))=x只有一个解x=0又f(0)=0,故0不是二阶周期点.
当 ![]() 时,有f(f(x))=
时,有f(f(x))= 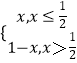 .
.
∴f(f(x))=x有解集,{x|x ![]() },故此集合中的所有点都不是二阶周期点.
},故此集合中的所有点都不是二阶周期点.
当 ![]() 时,有f(f(x))=
时,有f(f(x))= 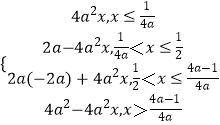 ,
,
∴f(f(x))=x有四个解:0, ![]() ,
, ![]() ,
, ![]() .
.
由f(0)=0, ![]() ,
, ![]() ,
, ![]() .
.
故只有 ![]() ,
, ![]() 是f(x)的二阶周期点,综上所述,所求a的取值范围为
是f(x)的二阶周期点,综上所述,所求a的取值范围为 ![]()
(3)解:由(2)得 ![]() ,
, ![]() .
.
∵x2为函数f(x)的最大值点,∴ ![]() ,或
,或 ![]() .
.
当 ![]() 时,S(a)=
时,S(a)= ![]()
![]()
![]() |
| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
求导得:S′(a)= 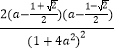 .
.
∴当 ![]() 时,S(a)单调递增,当
时,S(a)单调递增,当 ![]() 时,S(a)单调递减.
时,S(a)单调递减.
当 ![]() 时,S(a)=
时,S(a)= ![]() ,求导得
,求导得 ![]() .
.
∵ ![]() ,从而有
,从而有 ![]() .
.
∴当 ![]() 时,S(a)单调递增
时,S(a)单调递增
【解析】(1)只要证明 ![]() 成立即可;(2)对a分类讨论,利用二阶周期点的定义即可得出;(3)由(2)得出x3 , 得出三角形的面积,利用导数即可得出其单调性.
成立即可;(2)对a分类讨论,利用二阶周期点的定义即可得出;(3)由(2)得出x3 , 得出三角形的面积,利用导数即可得出其单调性.
【考点精析】根据题目的已知条件,利用函数的值和利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢
不喜欢
合计
大于45岁
26
6
32
25岁至45岁
13
15
28
合计
39
21
60
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:

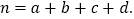

0.025
0.010
0.005
0,001

5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于不重合的两个平面
 与
与 ,给定下列条件:
,给定下列条件: ①存在平面
 ,使得
,使得 、
、 都垂直于
都垂直于 ;
;②存在平面
 ,使得
,使得 、
、 都平行于
都平行于 ;
;③
 内有不共线的三点到
内有不共线的三点到 的距离相等;
的距离相等;④存在异面直线
 ,
, ,使得
,使得 ,
, ,
, ,
,
其中,可以判定
 与
与 平行的条件有( )
平行的条件有( )A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆C:
 经过点P(1,
经过点P(1,  ),离心率e=
),离心率e=  ,直线l的方程为x=4.
,直线l的方程为x=4. 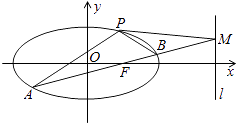
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1 , k2 , k3 . 问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
 中,圆
中,圆 与
与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与圆
分别与圆 交于
交于 ,
, 两点.
两点.
(Ⅰ)若
 ,
, ,求
,求 的面积;
的面积;(Ⅱ)若直线
 过点
过点 ,证明:
,证明: 为定值,并求此定值.
为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,且
,且 .
.(1)证明
 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;(2)求
 ;
;(3)设
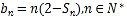 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种产品,每年投入固定成本
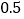 万元.此外,每生产
万元.此外,每生产 件这种产品还需要增加投入
件这种产品还需要增加投入 万元.经测算,市场对该产品的年需求量为
万元.经测算,市场对该产品的年需求量为 件,且当出售的这种产品的数量为
件,且当出售的这种产品的数量为 (单位:百件)时,销售所得的收入约为
(单位:百件)时,销售所得的收入约为 (万元).
(万元).(1)若该公司这种产品的年产量为
 (单位:百件),试把该公司生产并销售这种产品所得的年利润
(单位:百件),试把该公司生产并销售这种产品所得的年利润 表示为年产量
表示为年产量 的函数;
的函数;(2)当该公司的年产量
 为多少时,当年所得利润
为多少时,当年所得利润 最大?最大为多少?
最大?最大为多少?
相关试题

