【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢 | 不喜欢 | 合计 | |
大于45岁 | 26 | 6 | 32 |
25岁至45岁 | 13 | 15 | 28 |
合计 | 39 | 21 | 60 |
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:![]()
![]()
| 0.025 | 0.010 | 0.005 | 0,001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1) 有99.5%以上的把握认为喜欢中华传统文化与年龄有关;
(2) ![]() .
.
【解析】分析:(Ⅰ)根据列联表,计算观测值,对照临界值得出结论;
(Ⅱ)按年龄采用分层抽样方法求出大于45岁和不大于45岁应抽取的人数,用列举法计算所求的概率值.
详解:(Ⅰ)![]()
故有99.5%以上的把握认为喜欢中华传统文化与年龄有关;
(Ⅱ)从6人中任选2人,共15种不同结果,其中大于45岁的4人,25岁至45岁的2人,故选到的2人均大于45岁的不同结果有6种,故所求概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数


(1)当
 时,求过点
时,求过点 处的切线方程
处的切线方程(2)若函数
 有两个不同的零点,求
有两个不同的零点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的是__________.
①将一组数据中的每个数据都加上或减去同一个常数后,方差不变;
②在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“若某人吸烟,则他有99%的可能患肺病;”
③已知“
 ”为真命题,则“
”为真命题,则“ ”、“
”、“ ”、“
”、“ ”中至少有一个真命题;
”中至少有一个真命题;④以模型
 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设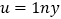 ,其变换后得到线性回归方程
,其变换后得到线性回归方程 则
则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中, 是棱
是棱 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)若
 是棱
是棱 的中点,求三棱锥
的中点,求三棱锥 的体积与三棱柱
的体积与三棱柱 的体积之比.
的体积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于不重合的两个平面
 与
与 ,给定下列条件:
,给定下列条件: ①存在平面
 ,使得
,使得 、
、 都垂直于
都垂直于 ;
;②存在平面
 ,使得
,使得 、
、 都平行于
都平行于 ;
;③
 内有不共线的三点到
内有不共线的三点到 的距离相等;
的距离相等;④存在异面直线
 ,
, ,使得
,使得 ,
, ,
, ,
,
其中,可以判定
 与
与 平行的条件有( )
平行的条件有( )A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆C:
 经过点P(1,
经过点P(1,  ),离心率e=
),离心率e=  ,直线l的方程为x=4.
,直线l的方程为x=4. 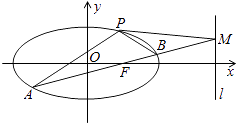
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1 , k2 , k3 . 问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,a为常数且a>0.
,a为常数且a>0.
(1)f(x)的图象关于直线x= 对称;
对称;
(2)若x0满足f(f(x0))=x0 , 但f(x0)≠x0 , 则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1 , x2 , 试确定a的取值范围;
(3)对于(2)中的x1 , x2 , 和a,设x3为函数f(f(x))的最大值点,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),记△ABC的面积为S(a),讨论S(a)的单调性.
相关试题

