【题目】空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为![]() 等六项.空气质量按照
等六项.空气质量按照![]() 大小分为六级:一级
大小分为六级:一级![]() 为优;二级
为优;二级![]() 为良好;三级
为良好;三级![]() 为轻度污染;四级
为轻度污染;四级![]() 为中度污染;五级
为中度污染;五级![]() 为重度污染;六级
为重度污染;六级![]() 为严重污染.
为严重污染.
某人根据环境监测总站公布的数据记录了某地某月连续10天![]() 的茎叶图如图所示:
的茎叶图如图所示:

(1)利用访样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);
(2)若从样本中的空气质量不佳(![]() )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
参考答案:
【答案】(1)15;(2)![]() .
.
【解析】【试题分析】
(1)依据题设条件运用茎叶图中的数据求解;(2)运用列举法及古典概型进行求解:
(1)从茎叶图中可发现该样本中空气质量优的天数为1,空气质量良的天数为4,故该样本中空气质量优良的频率为![]() ,
,
估计该月空气质量优良的频率![]() ,从而估计该月空气质量优良的天数为
,从而估计该月空气质量优良的天数为![]() .
.
(2)该样本中轻度污染共3天,分别记为![]() ;中度污染1天,记为
;中度污染1天,记为![]() ;重度污染1天,记为
;重度污染1天,记为![]() ,从中随机抽取三天的所有可能结果表示为:
,从中随机抽取三天的所有可能结果表示为:
![]() ;共10个;
;共10个;
其中空气质量互不相同的结果有:![]() ;共3个.
;共3个.
所以这两天的空气质量等级恰好不同的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的
 列联表:
列联表:爱好
不爱好
合计
男
20
30
50
女
10
20
30
合计
30
50
80
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为
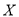 ,求
,求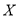 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
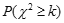
0.050
0.010

3.841
6.635
附:
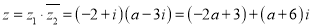
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=
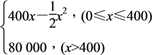
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少元?(总收益=总成本+利润)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
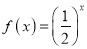 ,函数
,函数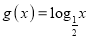 .
.(1)若
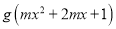 的定义域为
的定义域为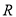 ,求实数
,求实数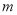 的取值范围;
的取值范围;(2)当
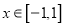 时,求函数
时,求函数 的最小值
的最小值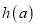 ;
;(3)是否存在非负实数
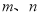 ,使得函数
,使得函数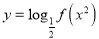 的定义域为
的定义域为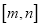 ,值域为
,值域为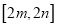 ,若存在,求出
,若存在,求出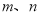 的值;若不存在,则说明理由.
的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径
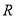
,此时圆内接正六边形的周长为
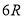
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据:
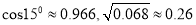
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
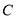 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在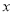 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为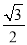 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
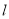 与椭圆
与椭圆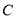 交于
交于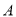 ,
, 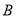 两点且
两点且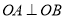 ,是否存在以原点
,是否存在以原点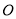 为圆心的定圆与直线
为圆心的定圆与直线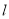 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件
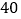 元,售价为每件
元,售价为每件 元,每个月可卖出
元,每个月可卖出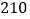 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨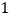 元,则每个月少卖
元,则每个月少卖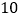 件(每件售价不能高于
件(每件售价不能高于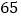 元).设每件商品的售价上涨
元).设每件商品的售价上涨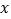 元(
元(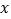 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为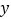 元.
元.(1)求
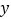 与
与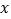 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量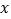 的取值范围;
的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
相关试题

