【题目】(理科)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为 “课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为 “课外体育达标”与性别有关?

(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的数学期望.
的数学期望.
独立性检验界值表:

(参考公式:  ,其中
,其中![]() )
)
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据所给的数据列出列联表,再代入公式计算得出![]() ,与临界值比较即可得出即结论;(2)由题意,用频率代替概率可得出抽到“课外体育达标”学生的频率为
,与临界值比较即可得出即结论;(2)由题意,用频率代替概率可得出抽到“课外体育达标”学生的频率为![]() ,由于
,由于![]() ,由公式计算出期望与方差即可.
,由公式计算出期望与方差即可.
试题解析:(1)列出列联表,
课外体育不达标 | 课外体育达标 | 合计 | |
男 | 60 | 30 | 90 |
女 | 90 | 20 | 110 |
合计 | 150 | 50 | 200 |
![]() ,
,
所以在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关.
(2)由表中数据可得,抽到“课外体育达标”学生的概率为0.25,
将频率视为概率,∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
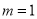 时,求函数
时,求函数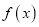 的单调区间与极值;
的单调区间与极值;(2)若
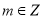 ,关于
,关于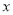 的不等式
的不等式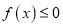 恒成立,求
恒成立,求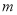 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
(1)求居民月用水量费用
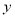 (单位:元)关于月用电量
(单位:元)关于月用电量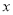 (单位:吨)的函数解析式;
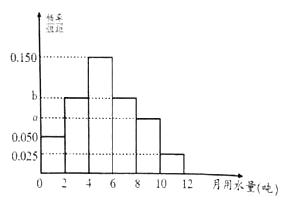
(单位:吨)的函数解析式;(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占60%,求
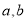 的值;
的值;(3)若地区居民用水量平均值超过6吨,则说明该地区居民用水没有节约意识在满足(2)的条件下,请你估计
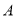 市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表). -
科目: 来源: 题型:
查看答案和解析>>【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据
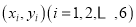 ,如下表所示:
,如下表所示:
已知
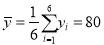 .
.(1)求出
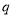 的值;
的值;(2)已知变量
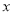 ,
, 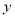 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量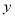 (件)关于试销单价
(件)关于试销单价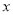 (元)的线性回归方程
(元)的线性回归方程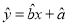 ;
;(3)用
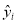 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与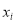 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据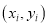 的残差的绝对值
的残差的绝对值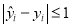 时,则将销售数据
时,则将销售数据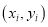 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数
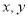 满足
满足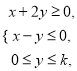 ,若目标函数
,若目标函数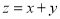 的最大值为6,则
的最大值为6,则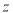 的最小值为( )
的最小值为( )A.
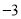 B.
B. 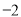 C.
C. 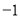 D. 0
D. 0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)已知的椭圆
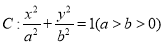 的左、右两个焦点分别为
的左、右两个焦点分别为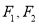 ,上顶点
,上顶点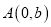 ,
, 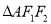 是正三角形且周长为6.
是正三角形且周长为6.(1)求椭圆
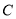 的标准方程及离心率;
的标准方程及离心率;(2)
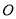 为坐标原点,
为坐标原点, 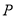 是直线
是直线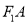 上的一个动点,求
上的一个动点,求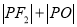 的最小值,并求出此时点
的最小值,并求出此时点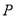 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(理科)在平面直角坐标系
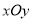 中,
中, 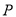 是椭圆
是椭圆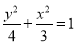 上的一个动点,点
上的一个动点,点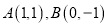 ,则
,则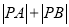 的最大值为( )
的最大值为( )A. 5 B. 4 C. 3 D. 2
相关试题

