【题目】已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF.则下列结论不正确的是( )
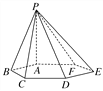
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
参考答案:
【答案】D
【解析】试题分析:由已知中六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC.根据正六边形的几何特征,根据线面平行和线面垂直的判定定理,对四个答案逐一进行判断,即可得到结论.
解:∵六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC.
则AF∥CD,由线面平行的判定定理,可得CD∥平面PAF,故A正确;
DF⊥AF,DF⊥PA,由线面垂直的判定定理可得DF⊥平面PAF,故B正确;
CF∥AB,由线面平行的判定定理,可得CF∥平面PAB,故C正确;
CF与AD不垂直,故D中,CF⊥平面PAD不正确;
故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知底角为
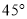 的等腰梯形
的等腰梯形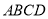 ,底边
,底边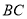 长为12,腰长为
长为12,腰长为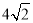 ,当一条垂直于底边
,当一条垂直于底边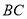 (垂足为
(垂足为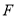 )的直线
)的直线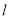 从左至右移动(与梯形
从左至右移动(与梯形 有公共点)时,直线
有公共点)时,直线 把梯形分成两部分.
把梯形分成两部分.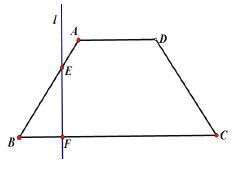
(1)令
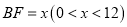 ,试写出直线右边部分的面积
,试写出直线右边部分的面积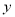 与
与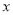 的函数解析式;
的函数解析式;(2)在(1)的条件下,令
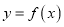 .构造函数
.构造函数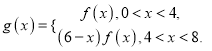
①判断函数
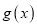 在
在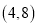 上的单调性;
上的单调性;②判断函数
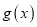 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
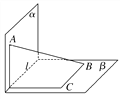
A. 30° B. 45°
C. 60° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
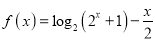 .
.(1)证明:对任意的
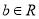 ,函数
,函数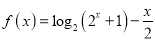 的图像与直线
的图像与直线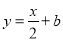 最多有一个交点;
最多有一个交点;(2)设函数
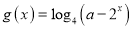 ,若函数
,若函数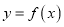 与函数
与函数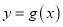 的图像至少有一个交点,求实数
的图像至少有一个交点,求实数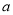 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
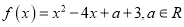
(1)若函数
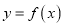 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;(2) 若函数
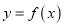 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;(3)设函数
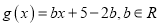 ,当
,当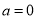 时,若对任意的
时,若对任意的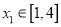 ,总存在
,总存在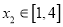 ,使得
,使得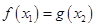 ,求b的取值范围.
,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域是
的定义域是 .
.(1)判断
 在
在 上的单调性,并证明;
上的单调性,并证明;(2)若不等式
 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
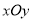 中,直线
中,直线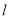 的参数方程是
的参数方程是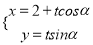 (
(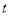 为参数),以
为参数),以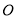 为极点,
为极点, 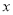 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线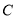 的极坐标方程为
的极坐标方程为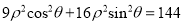 ,且直线
,且直线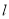 与曲线
与曲线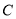 交于
交于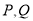 两点.
两点.(Ⅰ)求曲线
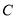 的直角坐标方程及直线
的直角坐标方程及直线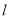 恒过的定点
恒过的定点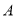 的坐标;
的坐标;(Ⅱ)在(Ⅰ)的条件下,若
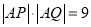 ,求直线
,求直线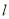 的普通方程.
的普通方程.
相关试题

