【题目】已知函数![]() 的定义域是
的定义域是![]() .
.
(1)判断![]() 在
在![]() 上的单调性,并证明;
上的单调性,并证明;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:首先要注意到大家熟知的常用的函数![]() ,第一定义域为R,第二这个函数是奇函数,第三它是单增函数,熟悉这3条,本题的第一步就只需按定义去证明了,有了函数的单调性,利用函数的单调性与奇偶性解不等式,利用极值原理求出参数的取值范围.
,第一定义域为R,第二这个函数是奇函数,第三它是单增函数,熟悉这3条,本题的第一步就只需按定义去证明了,有了函数的单调性,利用函数的单调性与奇偶性解不等式,利用极值原理求出参数的取值范围.
试题解析:
(1)因为函数![]() 的定义域为
的定义域为![]() ,对于函数
,对于函数![]() 定义域内的每一个
定义域内的每一个![]() ,都有
,都有
![]()
所以,函数![]() 是奇函数.
是奇函数.
设![]() 是
是![]() 上任意两个实数,且
上任意两个实数,且![]() ,则
,则
 .
.
由![]() ,得
,得![]() ,
, 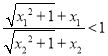 即
即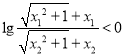 .
.
于是![]() ,
,
即![]() .
.
所以函数![]() 在
在![]() 上是増函数,且
上是増函数,且![]()
易证函数![]() 在
在![]() 上是増函数,且
上是増函数,且![]() .
.
∵![]()
∴函数![]() 在
在![]() 上是増函数.
上是増函数.
(2)![]() 等价于
等价于![]() ,即
,即![]()
原条件等价于![]() 对任意
对任意![]() 恒成立,
恒成立,
只需要![]() .
.
令![]() ,设函数
,设函数![]() .
.
由函数![]() 的单调性可知
的单调性可知![]() .
.
∴![]()
∴实数![]() 的取值范围
的取值范围![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
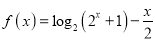 .
.(1)证明:对任意的
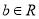 ,函数
,函数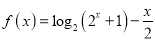 的图像与直线
的图像与直线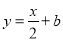 最多有一个交点;
最多有一个交点;(2)设函数
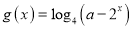 ,若函数
,若函数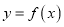 与函数
与函数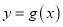 的图像至少有一个交点,求实数
的图像至少有一个交点,求实数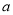 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF.则下列结论不正确的是( )
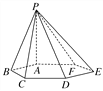
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
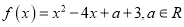
(1)若函数
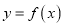 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;(2) 若函数
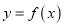 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;(3)设函数
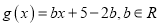 ,当
,当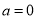 时,若对任意的
时,若对任意的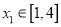 ,总存在
,总存在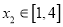 ,使得
,使得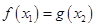 ,求b的取值范围.
,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
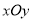 中,直线
中,直线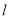 的参数方程是
的参数方程是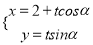 (
(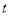 为参数),以
为参数),以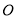 为极点,
为极点, 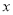 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线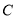 的极坐标方程为
的极坐标方程为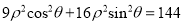 ,且直线
,且直线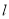 与曲线
与曲线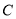 交于
交于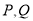 两点.
两点.(Ⅰ)求曲线
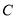 的直角坐标方程及直线
的直角坐标方程及直线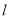 恒过的定点
恒过的定点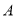 的坐标;
的坐标;(Ⅱ)在(Ⅰ)的条件下,若
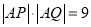 ,求直线
,求直线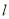 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
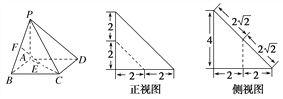
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为
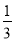 .
.(1)若出现故障的机器台数为
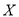 ,求
,求 的分布列;
的分布列;(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
相关试题

