【题目】已知函数![]() .
.
(1)证明:对任意的![]() ,函数
,函数![]() 的图像与直线
的图像与直线![]() 最多有一个交点;
最多有一个交点;
(2)设函数![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像至少有一个交点,求实数
的图像至少有一个交点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:两个函数图象的交点个数问题等价转化后为方程的解的个数讨论问题,针对参数b![]() 和
和![]() 两种情况进行讨论,研究图象的交点个数;当研究对数方程时,利用同底对数相等,只需真数大于零且相等,令
两种情况进行讨论,研究图象的交点个数;当研究对数方程时,利用同底对数相等,只需真数大于零且相等,令![]() 转化为二次方程的根的分布问题,根据判别式等要求,列不等式求解.
转化为二次方程的根的分布问题,根据判别式等要求,列不等式求解.
试题解析:
(1)证明:原问题等价于![]() 解的讨论.
解的讨论.
因为![]() ,即
,即![]() .
.
当![]() 时,方程无解,即两图像无交点;
时,方程无解,即两图像无交点;
当![]() 时,方程有一解,即两图像有一个交点,得证.
时,方程有一解,即两图像有一个交点,得证.
(2)函数![]() 与函数
与函数![]() 的图像至少有一个交点,等价于方程
的图像至少有一个交点,等价于方程
![]() 至少有一个解.即
至少有一个解.即![]() .
.
设![]() ,即方程
,即方程![]() 至少有一个正解.
至少有一个正解.
![]() 当
当![]() 时,即
时,即![]()
∵![]() ∴
∴![]() 不符合题意
不符合题意
当![]() 时,方程有一个正解,符合题意.
时,方程有一个正解,符合题意.
![]() 当
当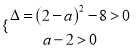 时,即
时,即![]() .此时方程有两个不同的正解.
.此时方程有两个不同的正解.
综上所述:实数![]() 的取值范围是
的取值范围是![]() .
.
![]() 转化成
转化成![]() .利用函数单调性也可以处理.
.利用函数单调性也可以处理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(1)证明:
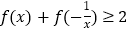 ;
;(2)若不等式
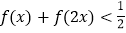 的解集是非空集,求
的解集是非空集,求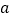 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知底角为
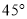 的等腰梯形
的等腰梯形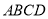 ,底边
,底边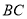 长为12,腰长为
长为12,腰长为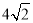 ,当一条垂直于底边
,当一条垂直于底边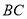 (垂足为
(垂足为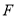 )的直线
)的直线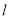 从左至右移动(与梯形
从左至右移动(与梯形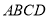 有公共点)时,直线
有公共点)时,直线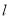 把梯形分成两部分.
把梯形分成两部分.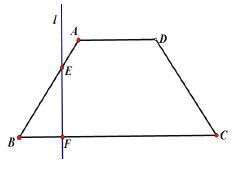
(1)令
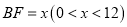 ,试写出直线右边部分的面积
,试写出直线右边部分的面积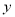 与
与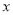 的函数解析式;
的函数解析式;(2)在(1)的条件下,令
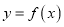 .构造函数
.构造函数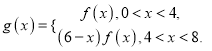
①判断函数
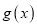 在
在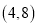 上的单调性;
上的单调性;②判断函数
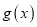 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
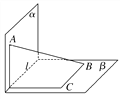
A. 30° B. 45°
C. 60° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF.则下列结论不正确的是( )
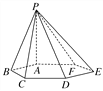
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
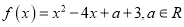
(1)若函数
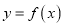 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;(2) 若函数
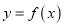 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;(3)设函数
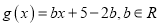 ,当
,当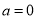 时,若对任意的
时,若对任意的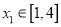 ,总存在
,总存在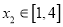 ,使得
,使得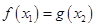 ,求b的取值范围.
,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域是
的定义域是 .
.(1)判断
 在
在 上的单调性,并证明;
上的单调性,并证明;(2)若不等式
 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
相关试题

