【题目】(1)设a,b是两个不相等的正数,若![]() ,用综合法证明:a+b>4
,用综合法证明:a+b>4
(2)已知a>b>c,且a+b+c=0,用分析法证明:![]() .
.
参考答案:
【答案】(1)详见解析(2)详见解析
【解析】试题分析:(1)综合法,从已知条件出发,利用定义、公理、定理、性质等,经过一系列的推理,论证而得出命题成立,这种证明方法称为综合法即“由因寻果”的方法;(2)分析法,从所要证明的结论出发,逐步寻求使它成立的充分条件,直至所需条件为已知条件或一个明显成立的事实,从而得出要证的命题成立,这种证明方法称为分析法,即“执果索因”的证明方法.
试题解析:(1)因为a>0,b>0,且a≠b,
所以a+b=(a+b)(![]() )=1+1+
)=1+1+![]() >2+2
>2+2![]() =4.所以a+b>4
=4.所以a+b>4
(2)因为a>b>c,且a+b+c=0,所以a>0,c<0,
要证明原不等式成立,只需证明![]()
即证b2-ac<3a2,又b=-(a+c),从而只需证明(a+c)2-ac<3a2,
即证(a-c)(2a+c)>0,
因为a-c>0,2a+c=a+c+a=a-b>0,
所以(a-c)(2a+c)>0成立,故原不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
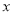 的方程
的方程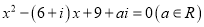 有实数根b.
有实数根b.(1)求实数
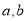 的值.
的值.(2)若复数
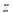 满足
满足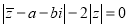 . 求z为何值时,|z|有最小值,并求出|z|的最小值.
. 求z为何值时,|z|有最小值,并求出|z|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+3x2+9x+1.
(1)求f(x)的单调递减区间;
(2)求f(x)在点(﹣2,f(﹣2))处的切线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
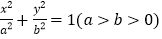 的离心率
的离心率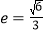 ,直线
,直线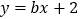 与圆
与圆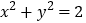 相切.
相切.(1)求椭圆的方程;
(2)已知定点
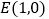 ,若直线
,若直线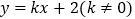 与椭圆相交于
与椭圆相交于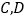 两点,试判断是否存在实数
两点,试判断是否存在实数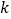 ,使得以
,使得以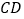 为直径的圆过定点
为直径的圆过定点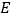 ?若存在,求出
?若存在,求出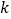 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品上市30天内每件的销售价格
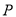 元与时间
元与时间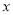 天函数关系是
天函数关系是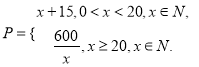 该商品的日销售量
该商品的日销售量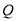 件与时间
件与时间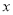 天函数关系是
天函数关系是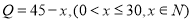 .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;(2)求这个商品的日销售金额的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
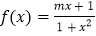 是
是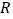 上的偶函数.
上的偶函数.(1)求实数
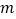 的值;
的值;(2)判断并证明函数
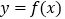 在
在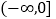 上单调性;
上单调性;(3)求函数
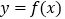 在
在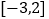 上的最大值与最小值.
上的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)全集U={2,4,-(a-3)2},集合A={2,a2-a+2},若UA={-1},求实数a的值. (2)已知A={x|2a≤x≤a+3},B={x|x<-1或x>5},若A∩B=,求a的取值范围.
相关试题

