【题目】已知椭圆![]() 的离心率
的离心率![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆的方程;
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,试判断是否存在实数
两点,试判断是否存在实数![]() ,使得以
,使得以![]() 为直径的圆过定点
为直径的圆过定点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在实数
;(2)存在实数![]() 使得以
使得以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
【解析】试题分析: (1)圆心到切线距离等于半径得![]() ,即
,即![]() ,再根据离心率
,再根据离心率![]() ,解得
,解得![]() ,(2)由以
,(2)由以![]() 为直径的圆过点
为直径的圆过点![]() ,得
,得![]() ,设坐标转化条件得
,设坐标转化条件得![]() ,将直线方程与椭圆方程联立,利用韦达定理得
,将直线方程与椭圆方程联立,利用韦达定理得![]() ,
,![]() ,代入条件并化简得
,代入条件并化简得![]() .
.
试题解析:(1)因为直线![]() :
:![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,
,
∴![]() ,
,
∵椭圆的离心率![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴所求椭圆的方程是![]() .
.
(2)直线![]() 代入椭圆方程,消去
代入椭圆方程,消去![]() 可得:
可得:![]()
∴![]() ,∴
,∴![]() 或
或![]() ,
,
设![]() ,则有
,则有![]() ,
,![]() ,
,
若以![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]() ,
,
解得![]() ,
,
所以存在实数![]() 使得以
使得以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
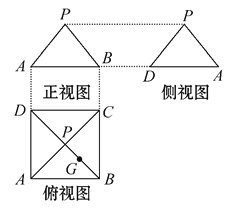
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
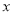 的方程
的方程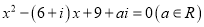 有实数根b.
有实数根b.(1)求实数
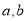 的值.
的值.(2)若复数
 满足
满足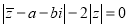 . 求z为何值时,|z|有最小值,并求出|z|的最小值.
. 求z为何值时,|z|有最小值,并求出|z|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+3x2+9x+1.
(1)求f(x)的单调递减区间;
(2)求f(x)在点(﹣2,f(﹣2))处的切线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)设a,b是两个不相等的正数,若
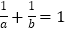 ,用综合法证明:a+b>4
,用综合法证明:a+b>4(2)已知a>b>c,且a+b+c=0,用分析法证明:
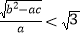 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品上市30天内每件的销售价格
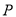 元与时间
元与时间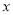 天函数关系是
天函数关系是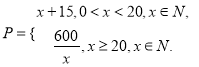 该商品的日销售量
该商品的日销售量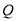 件与时间
件与时间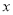 天函数关系是
天函数关系是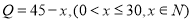 .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;(2)求这个商品的日销售金额的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
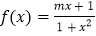 是
是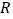 上的偶函数.
上的偶函数.(1)求实数
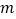 的值;
的值;(2)判断并证明函数
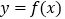 在
在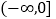 上单调性;
上单调性;(3)求函数
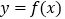 在
在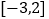 上的最大值与最小值.
上的最大值与最小值.
相关试题

